题目内容
已知正方形ABCD的边长为2,P为其外接圆上一动点,则
•
的最大值为( )
| AB |
| AP |
A、2+2
| ||
B、2+
| ||
C、2+2
| ||
D、2+
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:建立坐标系,利用向量的坐标运算、数量积运算和一次函数的单调性即可得出
解答:
解:如图所示,建立直角坐标系.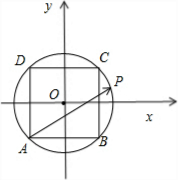
O(0,0),A(-1,-1),B(1,-1).
∴
=(1,-1)-(-1,-1)=(2,0).
设P(x,y),则x2+y2=2,(-
,
).
∴
=(x,y)-(-1,-1)=(x+1,y+1).
∴
•
=(2,0)•(x+1,y+1)=2(x+1),
∵-
≤x≤
,
∴当x=
时,
•
的最大值为2
+2.
故选为:A.

O(0,0),A(-1,-1),B(1,-1).
∴
| AB |
设P(x,y),则x2+y2=2,(-
| 2 |
| 2 |
∴
| AP |
∴
| AB |
| AP |
∵-
| 2 |
| 2 |
∴当x=
| 2 |
| AB |
| AP |
| 2 |
故选为:A.
点评:本题考查了向量的坐标运算、数量积运算和一次函数的单调性,关键是表示数量积才能够转化为函数求解,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列函数中,不具有奇偶性的是( )
| A、y=x2-1 | ||||
| B、y=sinxcosx | ||||
C、y=
| ||||
| D、y=lgx2 |
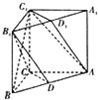 直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.
直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点. 如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本为S元.
如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本为S元.