题目内容
设集合M={x|x2-x-2≤0},N={y|y=x2,-1≤x≤2},则M∩N= .
考点:交集及其运算
专题:集合
分析:先求出x2-x-2≤0的解集M,由二次函数的性质求出集合N,再由交集的运算求出M∩N.
解答:
解:由x2-x-2≤0得,-1≤x≤2,则集合M=[-1,2],
因为y=x2,-1≤x≤2,所以0≤y≤4,则N=[0,4],
所以M∩N=[0,2],
故答案为[0,2].
因为y=x2,-1≤x≤2,所以0≤y≤4,则N=[0,4],
所以M∩N=[0,2],
故答案为[0,2].
点评:本题考查交集及其运算,以及一元二次不等式、一元二次函数的性质,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
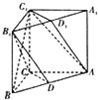 直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.
直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.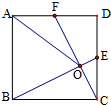 如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若
如图,在正方形ABCD中,E.F分别是CD.DA的中点,BE交CF于点O,若 若a=2,b=-1,则执行右边程序框图后输出的结果是
若a=2,b=-1,则执行右边程序框图后输出的结果是