题目内容
在平面直角坐标系中,已知直线l:ρcosθ+ρsinθ=2(θ为参数)和曲线C:
(t为参数),若l与C相交于A、B两点,则|AB|= .
|
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:把极坐标方程化为直角坐标方程、参数方程化为普通方程,联立解出交点坐标,利用两点之间的距离公式即可得出.
解答:
解:直线l:ρcosθ+ρsinθ=2(θ为参数),化为x+y=2,
把曲线C:
(t为参数),化为y=(x-2)2,
联立
化为x2-3x+2=0,
解得
,
.
取A(1,1),B(2,0),
∴|AB|=
=
.
故答案为:
.
把曲线C:
|
联立
|
解得
|
|
取A(1,1),B(2,0),
∴|AB|=
| (1-2)2+12 |
| 2 |
故答案为:
| 2 |
点评:本题考查了把极坐标方程化为直角坐标方程、参数方程化为普通方程、曲线的交点、两点之间的距离公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
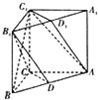 直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.
直三棱柱ABC-A1B1C1中,AC=CC1=BC=1,∠BCA=90°,D、D1分别是AB与A1B1的中点.(1)求异面直线AC1与A1B1所成的角的大小;
(2)求证:平面AC1D1∥平面B1CD.
在锐角三角形ABC中,角A,B,C对应的边长分别为a,b,c,若a,b,c成等比数列,则cosB的取值范围是( )
A、(0,
| ||||||
B、(0,
| ||||||
C、[
| ||||||
D、[
|
 如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本为S元.
如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本为S元. 若a=2,b=-1,则执行右边程序框图后输出的结果是
若a=2,b=-1,则执行右边程序框图后输出的结果是