题目内容
指出下列函数的单调区间,并说明在单调区间上是增函数还是减函数.
(1)f(x)=-x2+x-6;
(2)f(x)=-
;
(3)f(x)=
;
(4)f(x)=-x3+1.
(1)f(x)=-x2+x-6;
(2)f(x)=-
| 4 | x |
(3)f(x)=
| 3-2x |
| x |
(4)f(x)=-x3+1.
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据函数图象的形状即可得到其单调区间的单调性.
解答:
解:根据函数图象的形状即可得到其单调区间的单调性如下:
(1)f(x)=-x2+x-6的单调区间为(-∞,
)和[
,+∞),f(x)在(-∞,
)是增函数,f(x)在[
,+∞)上是减函数.
(2)f(x)=-
的单调区间为(0,+∞),f(x)在(0,+∞)上是减函数.
(3)f(x)=
的单调区间为(-∞,0)和(0,+∞),f(x)在(-∞,0)是减函数,在(0,+∞)上是减函数.
(4)f(x)=-x3+1的单调区间为(-∞,+∞),f(x)在(-∞,+∞)是减函数,
(1)f(x)=-x2+x-6的单调区间为(-∞,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)f(x)=-
| 4 | x |
(3)f(x)=
| 3-2x |
| x |
(4)f(x)=-x3+1的单调区间为(-∞,+∞),f(x)在(-∞,+∞)是减函数,
点评:本题主要考察了常见函数单调性的判断与证明,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
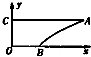 如图,A(e,1),B(1,0)是曲线y=lnx图象上的两点,点A在y轴上的射影为C,O为坐标原点,则曲线梯形OBAC的面积为( )
如图,A(e,1),B(1,0)是曲线y=lnx图象上的两点,点A在y轴上的射影为C,O为坐标原点,则曲线梯形OBAC的面积为( )| A、e | B、1 | C、e-1 | D、e-2 |
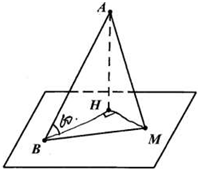 某风景区有空中景点A及平坦的地面上景点B.已知AB与地面所成角的大小为60°,点A在地面上的射影为H,如图,请在地面上选定点M,使得
某风景区有空中景点A及平坦的地面上景点B.已知AB与地面所成角的大小为60°,点A在地面上的射影为H,如图,请在地面上选定点M,使得