题目内容
已知函数f(x)=|x-3|+|x-a|,g(x)=x3+1,若函数y=f(g(x))的图象为轴对称图形,则实数a的值可能是 .
考点:函数的图象
专题:计算题,作图题,函数的性质及应用
分析:由题意,化简y=f(g(x))=|x3+1-3|+|x3+1-a|=|x3-2|+|x3+1-a|,讨论a的取值以去绝对值号,从而确定对称轴的可能取值,再取点检验,最后再判断即可.
解答:
解:y=f(g(x))=|x3+1-3|+|x3+1-a|
=|x3-2|+|x3+1-a|,
当1-a=-2,即a=3时,
y=2|x3-2|不是轴对称图形,
当1-a<-2;即a>3时,
由y=
;
若存在对称轴,则对称轴应为x=
;
而令y=1+a解得,x=0或x=
;
则
=
+
;
即
-
=
;
∵a>3;
∴
-
<
;
故不成立;
当1-a>-2;即a<3时,
由y=
;
若存在对称轴,则对称轴应为x=
;
而令y=1+a解得,x=0或x=
;
则
=
+
;
即
-
=
;
∵a<3;
∴当a=1或a=-1时,等号成立;
经检验,当a=1时,y=f(g(x))=|x3-2|+|x3|不对称,
当a=-1时,y=f(g(x))=|x3-2|+|x3+2|对称;

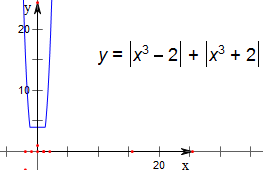
故答案为:-1.
=|x3-2|+|x3+1-a|,
当1-a=-2,即a=3时,
y=2|x3-2|不是轴对称图形,
当1-a<-2;即a>3时,
由y=
|
若存在对称轴,则对称轴应为x=
| ||||||
| 2 |
而令y=1+a解得,x=0或x=
| 3 | a+1 |
则
| 3 | a+1 |
| 3 | 2 |
| 3 | a-1 |
即
| 3 | a+1 |
| 3 | a-1 |
| 3 | 2 |
∵a>3;
∴
| 3 | a+1 |
| 3 | a-1 |
| 3 | 2 |
故不成立;
当1-a>-2;即a<3时,
由y=
|
若存在对称轴,则对称轴应为x=
| ||||||
| 2 |
而令y=1+a解得,x=0或x=
| 3 | a+1 |
则
| 3 | a+1 |
| 3 | 2 |
| 3 | a-1 |
即
| 3 | a+1 |
| 3 | a-1 |
| 3 | 2 |
∵a<3;
∴当a=1或a=-1时,等号成立;
经检验,当a=1时,y=f(g(x))=|x3-2|+|x3|不对称,
当a=-1时,y=f(g(x))=|x3-2|+|x3+2|对称;

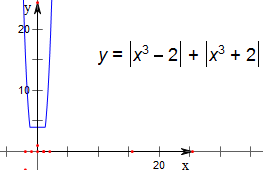
故答案为:-1.
点评:本题考查了图象的对称性的应用,考查了学生分类讨论的应用及作图能力,属于中档题.

练习册系列答案
相关题目
已知点P是平行四边形ABCD所在平面外一点,如果
=(2,-1,-4),
=(4,2,0),
=(-1,2,-1).对于结论:①AP⊥AB;②AP⊥AD;③
是平面ABCD的法向量;④
∥
.其中正确的个数是( )
| AB |
| AD |
| AP |
| AP |
| AP |
| BD |
| A、1 | B、2 | C、3 | D、4 |
已知焦点在x轴上的双曲线
-
=1的渐近线经过点P(1,
),则该双曲线的离心率是( )
| x2 |
| m |
| y2 |
| n |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
 已知f(x)=
已知f(x)= 已知直线l:y=kx-2与抛物线 C:x2=-2py(p>0)交于A、B两点,O为坐标原点
已知直线l:y=kx-2与抛物线 C:x2=-2py(p>0)交于A、B两点,O为坐标原点