题目内容
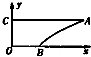 如图,A(e,1),B(1,0)是曲线y=lnx图象上的两点,点A在y轴上的射影为C,O为坐标原点,则曲线梯形OBAC的面积为( )
如图,A(e,1),B(1,0)是曲线y=lnx图象上的两点,点A在y轴上的射影为C,O为坐标原点,则曲线梯形OBAC的面积为( )| A、e | B、1 | C、e-1 | D、e-2 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:根据y=lnx,求出x=ey,根据题意可知曲线梯形OBAC的面积为直线y=1,与x轴,y轴,y=lnx的所围成的面积,故根据定积分即可求出面积
解答:
解:∵y=lnx,
∴x=ey,
根据题意可知曲线梯形OBAC的面积为直线y=1,与x轴,y轴,y=lnx的所围成的面积,
故S曲线梯形OBAC=
eydy=ey
=e-1,
故选:C
∴x=ey,

根据题意可知曲线梯形OBAC的面积为直线y=1,与x轴,y轴,y=lnx的所围成的面积,
故S曲线梯形OBAC=
| ∫ | 1 e |
| | | 1 0 |
故选:C
点评:本题考查了定积分的几何意义,属于基础题

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
已知点F为抛物线C:y2=4x的焦点,点P为准线l上的动点,直线PF交抛物线C于A,B两点,若P的纵坐标为m(m≠0),点D为准线为l与x轴的交点,则△DAB的面积S的取值范围为( )
| A、(1,4) |
| B、(1,8) |
| C、(4,+∞) |
| D、(8,+∞) |

多面体的三视图如图所示,则该多面体的表面积为(单位:cm)( )
A、28+4
| ||
B、30+4
| ||
C、30+4
| ||
D、28+4
|
在锐角△ABC中,∠A=2∠B,则
的取值范围为( )
| c |
| b |
| A、[1,2] |
| B、[1,3] |
| C、(1,3) |
| D、(1,2) |
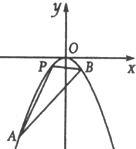 已知直线l:y=kx-2与抛物线 C:x2=-2py(p>0)交于A、B两点,O为坐标原点
已知直线l:y=kx-2与抛物线 C:x2=-2py(p>0)交于A、B两点,O为坐标原点