题目内容
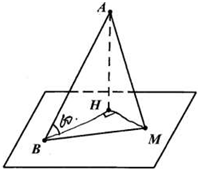某风景区有空中景点A及平坦的地面上景点B．已知AB与地面所成角的大小为60°，点A在地面上的射影为H，如图，请在地面上选定点M，使得| AB+BM |
| AM |
考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：根据正弦定理以及三角公式，将三角形的边长关系转化为角的关系，结合三角函数的辅助角公式即可得到结论．
解答：
解：∵AB与地面所成角的大小为60°，AH垂直于地面，BM是地面上的直线，
∴∠ABH=60°，∠ABM≥60°，
∵
=
=
，
∴
=
=
=
=
•sinM+cosM=
•sinM+cosM=cot
sinM+cosM≤cot30°sinM+cosM
=
sinM+cosM=2sin（M+30°），
当∠M=∠B=60°时，
达到最大值．
即当M在BH的延长上，且BH=HM处，
达到最大值．
∴∠ABH=60°，∠ABM≥60°，
∵
| AB |
| sinM |
| BM |
| sinA |
| AM |
| sinN |
∴
| AB+BM |
| AM |
| sinM+sinA |
| sinB |
| sinM+sin(B+M) |
| sinB |
| sinM+sinBcosM+cosBsinM |
| sinB |
=
| 1+cosB |
| sinB |
2cos2
| ||||
2sin
|
| B |
| 2 |
=
| 3 |
当∠M=∠B=60°时，
| AB+BM |
| AM |
即当M在BH的延长上，且BH=HM处，
| AB+BM |
| AM |
点评：本题主要考查空间正弦定理的应用以及三角函数的公式化简，综合性较强，难度较大．
练习册系列答案
相关题目
已知点F为抛物线C：y2=4x的焦点，点P为准线l上的动点，直线PF交抛物线C于A，B两点，若P的纵坐标为m（m≠0），点D为准线为l与x轴的交点，则△DAB的面积S的取值范围为（ ）
| A、（1，4） |
| B、（1，8） |
| C、（4，+∞） |
| D、（8，+∞） |
多面体的三视图如图所示，则该多面体的表面积为（单位：cm）（ ）
A、28+4
| ||
B、30+4
| ||
C、30+4
| ||
D、28+4
|
在锐角△ABC中，∠A=2∠B，则
的取值范围为（ ）
| c |
| b |
| A、[1，2] |
| B、[1，3] |
| C、（1，3） |
| D、（1，2） |