题目内容
对任意的实数x恒有3sin2x-cos2x+4acosx+a2≤31,则实数a的取值范围是 .
考点:三角函数的最值
专题:三角函数的求值
分析:设y=3sin2x-cos2x+4acosx+a2=3+2a2-4(cosx-
)2,再分a∈[-2,2]时、当a<-2时、当a>2时三种情况,分别利用二次函数的性质求得y的最大值,再根据y的最大值小于或等于31,求得a的范围,综合可得结论.
| a |
| 2 |
解答:
解:设y=3sin2x-cos2x+4acosx+a2=3-4cos2x+4acosx+a2=3+2a2-4(cosx-
)2,
当a∈[-2,2]时,
∈[-1,1],故当cosx=
时,函数y取得最大值为3+2a2,
再根据3+2a2≤31,求得-
≤a≤
.
当a<-2时,
<-1,故当cosx=-1时,函数y取得最大值为a2-4a-1,再根据a2-4a-1≤31,求得-4≤a<-2.
当a>2时,
>1,故当cosx=1时,函数y取得最大值为a2-4a-1,再根据a2-4a-1≤31,求得2<a≤4.
综上可得,a的范围为[-4,4],
故答案为:[-4,4].
| a |
| 2 |
当a∈[-2,2]时,
| a |
| 2 |
| a |
| 2 |
再根据3+2a2≤31,求得-
| 14 |
| 14 |
当a<-2时,
| a |
| 2 |
当a>2时,
| a |
| 2 |
综上可得,a的范围为[-4,4],
故答案为:[-4,4].
点评:本题主要考查同角三角函数的基本关系,二次函数的性质,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
偶函数f(x)在[-1,0]上为减函数,A、B为某个锐角三角形的两个内角,则( )
| A、f(cosA)>f(cosB) |
| B、f(sinA)>f(sinB) |
| C、f(sinA)>f(cosB) |
| D、f(sinA)<f(cosB) |
若在(x+
)n的展开式中,各系数之和为A,各二项式系数之和为B,且A+B=72,则n的值为( )
| 3 |
| x |
| A、3 | B、4 | C、5 | D、6 |
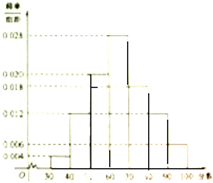 某校高一年级共有800名学生,其中男生480名,女生320名,在某次满分为100分的数学考试中,所有学生成绩在30分及30分以上,成绩在“80分及80分以上”的学生视为优秀.现按性别采用分层抽样的方法共抽取100名学生,将他们的成绩按[30,40]、[40,50]、[50,60]、[60,70]、[70,80]、[80,90]、[90,100]分成七组.得到的频率分布直方图如图所示:
某校高一年级共有800名学生,其中男生480名,女生320名,在某次满分为100分的数学考试中,所有学生成绩在30分及30分以上,成绩在“80分及80分以上”的学生视为优秀.现按性别采用分层抽样的方法共抽取100名学生,将他们的成绩按[30,40]、[40,50]、[50,60]、[60,70]、[70,80]、[80,90]、[90,100]分成七组.得到的频率分布直方图如图所示: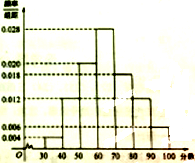 某校高一年级共有800名学生,其中男生480名,女生320名,在某次满分为100分的数学考试中,所有学生成绩在30分及30分以上,成绩在“80分及80分以上”的学生视为优秀,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100)分成七组,得到的频率分布直方图如图所示:
某校高一年级共有800名学生,其中男生480名,女生320名,在某次满分为100分的数学考试中,所有学生成绩在30分及30分以上,成绩在“80分及80分以上”的学生视为优秀,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100)分成七组,得到的频率分布直方图如图所示:


