题目内容
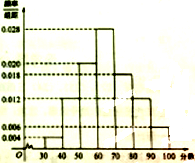 某校高一年级共有800名学生,其中男生480名,女生320名,在某次满分为100分的数学考试中,所有学生成绩在30分及30分以上,成绩在“80分及80分以上”的学生视为优秀,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100)分成七组,得到的频率分布直方图如图所示:
某校高一年级共有800名学生,其中男生480名,女生320名,在某次满分为100分的数学考试中,所有学生成绩在30分及30分以上,成绩在“80分及80分以上”的学生视为优秀,现按性别采用分层抽样的方法抽取100名学生,将他们的成绩按[30,40)、[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100)分成七组,得到的频率分布直方图如图所示:(Ⅰ)估计该年纪本次数学考试成绩的平均分(同一组中的数据用该区间中点值做代表);
(Ⅱ)请将下列2×2列联表补充完整,计算并说明是否有95%的把握认为“该校学生数学成绩优秀与性别有关”.
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | 12 | ||
| 女生 | |||
| 合计 | 100 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2>k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
考点:独立性检验,频率分布直方图
专题:应用题,概率与统计
分析:(Ⅰ)利用同一组中的数据用该区间中点值做代表,即可估计该年纪本次数学考试成绩的平均分;
(Ⅱ)应抽取男生60人,女生40人,可得2×2列联表,由列联表中数据,代入公式,求出K2的值,进而与临界值比较,即可得出结论.
(Ⅱ)应抽取男生60人,女生40人,可得2×2列联表,由列联表中数据,代入公式,求出K2的值,进而与临界值比较,即可得出结论.
解答:
解:(Ⅰ)估计该年纪本次数学考试成绩的平均分为0.04×35+0.12×45+0.2×55+0.28×65+0.18×75+0.12×85+0.06×95=65.4(分);
(Ⅱ)应抽取男生60人,女生40人,可得2×2列联表
K2=
≈0.407<3.841,
∴没有95%的把握认为“该校学生数学成绩优秀与性别有关”.
(Ⅱ)应抽取男生60人,女生40人,可得2×2列联表
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | 12 | 48 | 60 |
| 女生 | 6 | 34 | 40 |
| 合计 | 18 | 82 | 100 |
| 100(2×34-6×48)2 |
| 18×82×40×60 |
∴没有95%的把握认为“该校学生数学成绩优秀与性别有关”.
点评:本题考查独立性检验的应用,考查数据处理能力、运算求解能力和应用意识,本题解题的关键是正确运算出观测值,理解临界值对应的概率的意义,要想知道两个变量之间的有关或无关的精确的可信程度,只有利用独立性检验的有关计算,才能做出判断,本题是一个基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若loga
<1,则a的取值范围是( )
| 1 |
| 3 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
设集合A={x||x|<2},若B⊆A,则集合B可以是( )
| A、{x|-1<x<0} |
| B、{x|-1<x<3} |
| C、{x|-3<x<2} |
| D、{x|-3<x<3} |
执行如图所示框图,则输出S的值为( )


A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知a=3-
,b=log2
,c=log23,则( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、c>b>a |