题目内容
若集合{x|x+a=a|x|，x∈R}为单元素集，则实数a的取值范围是 ．
考点：函数的零点,集合的表示法
专题：计算题,函数的性质及应用
分析：当a=0时，方程x+a=a|x|①的解为x=0，满足条件；当a≠0时显然0不是其解，①的解为当x＞0时x=
，当x＜0时，x=-
，对a的取值分类讨论，即可确定实数a的取值范围．
| a |
| a-1 |
| a |
| a+1 |
解答：
解：当a=0时，方程x+a=a|x|①的解为x=0，满足条件；
当a≠0时显然0不是其解，①的解为当x＞0时x=
，当x＜0时，x=-
下面对a的取值分类讨论
当0＜a＜1时x=
，（舍去）x=-
＜0满足条件；
当a=1时①只有一解为，x=-
满足条件；
当a＞1时显然方程有二解舍去
当-1≤a＜0时①只有一根为x=
，当a＜-1时①有二解x=
，x=-
（舍去）．
综上a的范围是-1≤a≤1
故答案为：-1≤a≤1．
当a≠0时显然0不是其解，①的解为当x＞0时x=
| a |
| a-1 |
| a |
| a+1 |
下面对a的取值分类讨论
当0＜a＜1时x=
| a |
| a-1 |
| a |
| a+1 |
当a=1时①只有一解为，x=-
| a |
| a+1 |
当a＞1时显然方程有二解舍去
当-1≤a＜0时①只有一根为x=
| a |
| a-1 |
| a |
| a-1 |
| a |
| a+1 |
综上a的范围是-1≤a≤1
故答案为：-1≤a≤1．
点评：本题考查实数a的取值范围，考查分类讨论的数学思想，考查学生分析解决问题的能力，比较基础．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
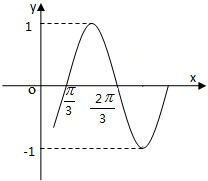若函数y=Asin（ωx+φ）在平面直角坐标系中的图象（部分）如图所示，其中ω＞0，|φ|≤π．