题目内容
甲乙两位同学参加学校安排的3次体能测试,规定按顺序测试,一旦测试合格就不必参加以后的测试,否则3次测试都要参加.甲同学3次测试每次合格的概率组成一个公差为
的等差数列,他第一次测试合格的概率不超过
,且他直到第二次测试才合格的概率为
,乙同学3次测试每次测试合格的概率均为
,每位同学参加的每次测试是否合格相互独立.
(Ⅰ)求甲同学第一次参加测试就合格的概率P;
(Ⅱ)设甲同学参加测试的次数为m,乙同学参加测试的次数为n,求ξ=m+n的分布列.
| 1 |
| 8 |
| 1 |
| 2 |
| 9 |
| 32 |
| 2 |
| 3 |
(Ⅰ)求甲同学第一次参加测试就合格的概率P;
(Ⅱ)设甲同学参加测试的次数为m,乙同学参加测试的次数为n,求ξ=m+n的分布列.
考点:离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)由甲同学3次测试每次合格的概率组成一个公差为
的等差数列,又甲同学第一次参加测试就合格的概率为P,故而甲同学参加第二、三次测试合格的概率分别是p+
、p+
,由题意知,(1-p)(p+
)=
,由此能求出甲同学第一次参加测试就合格的概率.
(Ⅱ)甲同学参加第二、三次测试合格的概率分别是
、
,由题意知,ξ的可能取值为2,3,4,5,6,分别求出相应的概率,由此能求出ξ=m+n的分布列.
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 8 |
| 9 |
| 32 |
(Ⅱ)甲同学参加第二、三次测试合格的概率分别是
| 3 |
| 8 |
| 1 |
| 2 |
解答:
解:(Ⅰ)由甲同学3次测试每次合格的概率组成一个公差为
的等差数列,
又甲同学第一次参加测试就合格的概率为P,
故而甲同学参加第二、三次测试合格的概率分别是p+
、p+
,
由题意知,(1-p)(p+
)=
,解得p=
或p=
(舍),
所以甲同学第一次参加测试就合格的概率为
.…(4分)
(Ⅱ)由(Ⅰ)知甲同学参加第二、三次测试合格的概率分别是
、
,
由题意知,ξ的可能取值为2,3,4,5,6,由题意可知
P(ξ=2)=
×
=
,
P(ξ=3)=
×(
×
)+(
×
)×
=
,
P(ξ=4)=
×(
×
)+(
×
)(
×
)+(
×
)×
=
,
P(ξ=5)=(
×
)×(
×
)+(
×
)×(
×
)=
,
P(ξ=6)=(
×
)×(
×
)=
,
所以ξ的分布列为:
…(12分)
| 1 |
| 8 |
又甲同学第一次参加测试就合格的概率为P,
故而甲同学参加第二、三次测试合格的概率分别是p+
| 1 |
| 8 |
| 1 |
| 4 |
由题意知,(1-p)(p+
| 1 |
| 8 |
| 9 |
| 32 |
| 1 |
| 4 |
| 5 |
| 8 |
所以甲同学第一次参加测试就合格的概率为
| 1 |
| 4 |
(Ⅱ)由(Ⅰ)知甲同学参加第二、三次测试合格的概率分别是
| 3 |
| 8 |
| 1 |
| 2 |
由题意知,ξ的可能取值为2,3,4,5,6,由题意可知
P(ξ=2)=
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 6 |
P(ξ=3)=
| 1 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 8 |
| 2 |
| 3 |
| 35 |
| 144 |
P(ξ=4)=
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 8 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 5 |
| 8 |
| 2 |
| 3 |
| 58 |
| 144 |
P(ξ=5)=(
| 3 |
| 4 |
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| 5 |
| 8 |
| 1 |
| 3 |
| 2 |
| 3 |
| 13 |
| 96 |
P(ξ=6)=(
| 3 |
| 4 |
| 5 |
| 8 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 96 |
所以ξ的分布列为:
| ξ | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|
点评:本题考查概率的求法,考查离散型随机变量的分布列的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知中心在原点,焦点在y轴上的双曲线的离心率为
,则它的渐近线方程为( )
| 5 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
已知关于x的方程2sin(x+
)-a=0在区间[0,2π]上有两个不同的实根,则实数a的数值范围是( )
| π |
| 3 |
| A、(-2,2) | ||||
| B、[-2,2] | ||||
C、[-2,
| ||||
D、(-2,
|
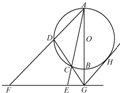 如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.
如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.