题目内容
已知数列{an}满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),求数列{an}的通项公式.(可能用到的结论:1×2×3×4×…×n=n!)
考点:数列递推式
专题:等差数列与等比数列
分析:由an=a1+2a2+3a3+…+(n-1)an-1(n≥2),an+1=a1+2a2+3a3+…+nan,可得an+1=(n+1)an.当n=2时,a2=a1=1.当n≥2时,利用“累乘求积”即可得出.
解答:
解:∵an=a1+2a2+3a3+…+(n-1)an-1(n≥2),
∴an+1=a1+2a2+3a3+…+nan,
∴an+1-an=nan,
∴an+1=(n+1)an.
当n=2时,a2=a1=1.
∴当n≥2时,
an=
•
•…•
•a2=n×(n-1)×…×3×1=
×n!.
∴an=
.
∴an+1=a1+2a2+3a3+…+nan,
∴an+1-an=nan,
∴an+1=(n+1)an.
当n=2时,a2=a1=1.
∴当n≥2时,
an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a3 |
| a2 |
| 1 |
| 2 |
∴an=
|
点评:本题考查了递推式的应用、“累乘求积”、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
在正四棱锥P-ABCD中,PA=
AB,M是BC的中点,G是△PAD的重心,则在平面PAD中经过点G且与直线PM垂直的直线条数有( )
| ||
| 2 |
| A、0条 | B、1条 | C、3条 | D、无数条 |
一个圆锥的表面积为π,它的侧面展开图是圆心角为120°的扇形,则该圆锥的高为( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
数列an=
的前5项之和是( )
| 1+(-1)n |
| 2 |
| A、0 | B、2 | C、4 | D、6 |
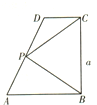 如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设