题目内容
11.已知△ABC的内角A,B,C所对的边分别为a,b,c,若A=30°,a=1,则$\frac{b+c}{sinB+sinC}$等于( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由已知及正弦定理可求b=2sinB,c=2sinC,化简所求即可计算得解.
解答 解:∵A=30°,a=1,
∴由正弦定理可得:$\frac{b}{sinB}=\frac{c}{sinC}=\frac{1}{sin30°}=2$,可得:b=2sinB,c=2sinC,
∴$\frac{b+c}{sinB+sinC}$=$\frac{2sinB+2sinC}{sinB+sinC}$=2.
故选:B.
点评 本题主要考查了特殊角的三角函数值,正弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
16.已知函数f(x)=lgx,0<a<b,若p=f($\sqrt{ab}$),q=f($\frac{a+b}{2}$),r=$\frac{1}{2}$[f(a)+f(b)],则p,q,r的大小关系是( )
| A. | p=r>q | B. | p=r<q | C. | q=r<p | D. | q-r>p |
20.“一条直线l与平面α内无数条直线异面”是“这条直线与平面α平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
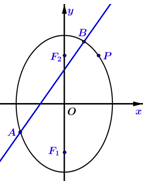 设椭圆$M:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)经过点$P(1,\sqrt{2})$,其离心率与双曲线x2-y2=1的离心率互为倒数.
设椭圆$M:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)经过点$P(1,\sqrt{2})$,其离心率与双曲线x2-y2=1的离心率互为倒数.