题目内容
2.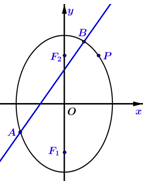 设椭圆$M:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)经过点$P(1,\sqrt{2})$,其离心率与双曲线x2-y2=1的离心率互为倒数.
设椭圆$M:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)经过点$P(1,\sqrt{2})$,其离心率与双曲线x2-y2=1的离心率互为倒数.(Ⅰ)求椭圆M的方程;
(Ⅱ) 动直线$l:y=\sqrt{2}x+m$交椭圆M于A、B两点,求△PAB面积的最大值.
分析 (Ⅰ)双曲线的离心率为$\sqrt{2}$,则椭圆的离心率为$e=\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,将$P(1,\sqrt{2})$代入椭圆方程,即可求得a和b的值,即可求得椭圆M的方程;
(Ⅱ) 将直线$l:y=\sqrt{2}x+m$代入椭圆方程,由韦达定理及弦长公式求得丨AB丨,则P到AB的距离为d=$\frac{丨m丨}{\sqrt{3}}$,则利用三角形的面积公式及韦达定理即可求得△PAB面积的最大值.
解答 解:(Ⅰ)双曲线的离心率为$\sqrt{2}$,则椭圆的离心率为$e=\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,由椭圆经过点$P(1,\sqrt{2})$,
得$\left\{\begin{array}{l}\frac{{{{\sqrt{2}}^2}}}{a^2}+\frac{1^2}{b^2}=1\\{a^2}={b^2}+{c^2}\\ \frac{c}{a}=\frac{{\sqrt{2}}}{2}\end{array}\right.$,解得:$\left\{\begin{array}{l}a=2\\ c=\sqrt{2}\\ b=\sqrt{2}\end{array}\right.$,
∴椭圆M的方程为 $\frac{y^2}{4}+\frac{x^2}{2}=1$.…(4分)
(Ⅱ)由$\left\{\begin{array}{l}{y=\sqrt{2}x+m}\\{\frac{{y}^{2}}{4}+\frac{{x}^{2}}{2}=1}\end{array}\right.$,得$4{x^2}+2\sqrt{2}mx+{m^2}-4=0$,
由△=(2$\sqrt{2}$m)2-16(m2-4)>0,得,$-2\sqrt{2}<m<2\sqrt{2}$,设A(x1,y1),B(x2,y2),
∴${x_1}+{x_2}=-\frac{{\sqrt{2}}}{2}m$,${x_1}{x_2}=\frac{{{m^2}-4}}{4}$.
∴$|AB|=\sqrt{1+2}|{x_1}-{x_2}|=\sqrt{3}•\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$\sqrt{3}•\sqrt{\frac{1}{2}{m^2}-{m^2}+4}=\sqrt{3}\sqrt{4-\frac{m^2}{2}}$.
又P到AB的距离为d=$\frac{丨m丨}{\sqrt{3}}$.
则${S_{△ABC}}=\frac{1}{2}|AB|d=\frac{1}{2}\sqrt{3}\sqrt{4-\frac{m^2}{2}}\frac{|m|}{{\sqrt{3}}}=\frac{1}{2}\sqrt{{m^2}(4-\frac{m^2}{2})}=\frac{1}{{2\sqrt{2}}}\sqrt{{m^2}(8-{m^2})}$…(10分)
∴${S_{△ABC}}≤\frac{1}{{2\sqrt{2}}}•\frac{{{m^2}+(8-{m^2})}}{2}=\sqrt{2}$当且仅当$m=±2∈(-2\sqrt{2},2\sqrt{2})$取等号.
∴${({S_{△ABC}})_{max}}=\sqrt{2}$.…(12分)
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理,弦长公式及基本不等式的应用,考查计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (-e2,+∞) | B. | (-e2,0) | C. | (-e-2,+∞) | D. | (-e-2,0) |
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | B. | 若$\overrightarrow{a}$=(1,k),$\overrightarrow{b}$=(-2,6),$\overrightarrow{a}$∥$\overrightarrow{b}$,则k=$\frac{1}{3}$ | ||
| C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 | D. | 若$\overrightarrow{a}$与$\overrightarrow{b}$是单位向量,则$\overrightarrow{a}$•$\overrightarrow{b}$=1 |
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [-$\sqrt{2}$,$\sqrt{6}$] | C. | [-$\sqrt{6}$,$\sqrt{6}$] | D. | [-$\sqrt{6}$,$\sqrt{2}$] |
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
| A. | (0,1) | B. | (-∞,0) | C. | [1,+∞) | D. | [0,1) |
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |