题目内容
16.已知函数f(x)=lgx,0<a<b,若p=f($\sqrt{ab}$),q=f($\frac{a+b}{2}$),r=$\frac{1}{2}$[f(a)+f(b)],则p,q,r的大小关系是( )| A. | p=r>q | B. | p=r<q | C. | q=r<p | D. | q-r>p |
分析 直接利用对数的运算性质可得p=r,再由基本不等式及对数函数的单调性可得p<q,则答案可求.
解答 解:∵p=f($\sqrt{ab}$)=lg$\sqrt{ab}$=$\frac{1}{2}$(lga+lgb),
r=$\frac{1}{2}$[f(a)+f(b)]=$\frac{1}{2}$(lga+lgb),
∴p=r,
又q=f($\frac{a+b}{2}$)=lg$\frac{a+b}{2}$,
而$\frac{a+b}{2}>\sqrt{ab}$,∴q>p=r.
故选:B.
点评 本题考查对数的运算性质,考查了基本不等式的应用,是基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
6.若复数$z=\frac{1-i}{i}$(i为虚数单位),则z的共轭复数$\overline z$=( )
| A. | 1+i | B. | -1+i | C. | l-i | D. | -1一i |
7.方程x2+2x+n2=0(n∈[-1,2])有实根的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
11.已知△ABC的内角A,B,C所对的边分别为a,b,c,若A=30°,a=1,则$\frac{b+c}{sinB+sinC}$等于( )
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
1.已知等差数列{an}满足a2=2,点(a4,a6)在直线x+2y-16=0上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+2${\;}^{{a}_{n}}$,求数列{bn}的前n项和Sn.
8.两圆x2+y2-4x+2y+1=0与x2+y2+4x-4y-1=0的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
5.在△OMN中,点A在OM上,点B在ON上,且AB∥MN,2OA=OM,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则终点P落在四边形ABNM内(含边界)时,$\frac{y+x+2}{x+1}$的取值范围是( )
| A. | $[\frac{1}{2},2]$ | B. | $[\frac{1}{3},3]$ | C. | $[\frac{3}{2},3]$ | D. | $[\frac{4}{3},4]$ |
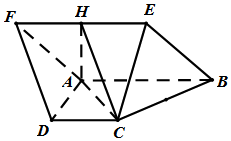 如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点
如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点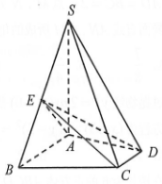 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点.