题目内容
19.已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-2x+x+m,则f(-2)=1.分析 根据奇函数的性质,可得m的值,进而求出函数的解析式,再由f(-2)=-f(2)得到答案.
解答 解:∵f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-2x+x+m,
∴f(0)=-1+m=0,
解得:m=1,
∴f(x)=-2x+x+1,
故f(2)=-1
f(-2)=-f(2)=1,
故答案为:1
点评 本题考查的知识点是抽象函数及其应用,函数的奇偶性,函数求值,难度中档.

练习册系列答案
相关题目
10.关于平面向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$,下列判断中正确的是( )
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | B. | 若$\overrightarrow{a}$=(1,k),$\overrightarrow{b}$=(-2,6),$\overrightarrow{a}$∥$\overrightarrow{b}$,则k=$\frac{1}{3}$ | ||
| C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 | D. | 若$\overrightarrow{a}$与$\overrightarrow{b}$是单位向量,则$\overrightarrow{a}$•$\overrightarrow{b}$=1 |
7.方程x2+2x+n2=0(n∈[-1,2])有实根的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
14.设集合A={x|x<0},B={x|x2-x≥0},则A∩B=( )
| A. | (0,1) | B. | (-∞,0) | C. | [1,+∞) | D. | [0,1) |
11.已知△ABC的内角A,B,C所对的边分别为a,b,c,若A=30°,a=1,则$\frac{b+c}{sinB+sinC}$等于( )
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
8.两圆x2+y2-4x+2y+1=0与x2+y2+4x-4y-1=0的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
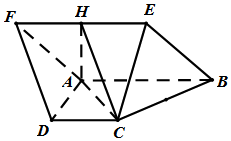 如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点
如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点