题目内容
1.数列{an}满足a1=1,(a1+a2)+(a2+a3)+(a3+a4)+…+(an+an+1)=2n+1-2,则a8=85.分析 (a1+a2)+(a2+a3)+(a3+a4)+…+(an+an+1)=2n+1-2,n≥2时,(a1+a2)+(a2+a3)+(a3+a4)+…+(an-1+an)=2n-2,可得an+an+1=2n.进而得到an+1-an-1=2n-1.利用“累加求和”方法即可得出.
解答 解:(a1+a2)+(a2+a3)+(a3+a4)+…+(an+an+1)=2n+1-2,
n≥2时,(a1+a2)+(a2+a3)+(a3+a4)+…+(an-1+an)=2n-2,
∴an+an+1=2n.
n≥3时,an-1+an=2n-1.
∴an+1-an-1=2n-1.
∵a1=1,可得a2=22-2-1=1.
则a8=(a8-a6)+(a6-a4)+(a4-a2)+a2=26+24+22+1=$\frac{{4}^{4}-1}{4-1}$=85.
故答案为:85.
点评 本题考查了等比数列的通项公式与求和公式及其性质、数列的递推关系、累加求和方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
11.设集合M={x|(x-1)(x+2)<0},N={x∈Z||x|≤2},则M∩N=( )
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
12.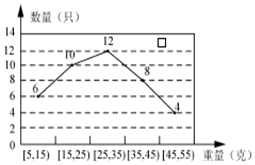 某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:
某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.
 某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:
某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
| 等级 | 一等品 | 二等品 | 三等品 |
| 重量(g) | [5,25) | [25,45) | [45,55] |
6.已知集合A={x|x2-2x-3≥0},B={x|-2≤x≤2},则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|-1≤x≤2} | C. | {x|-1≤x≤1} | D. | {x|-2≤x≤-1} |
13.已知数列{an}是等差数列,其前n项和Sn有最大值,且$\frac{{{a_{2017}}}}{{{a_{2016}}}}$<-1,则使得Sn>0的n的最大值为( )
| A. | 2016 | B. | 2017 | C. | 4031 | D. | 4033 |
10.已知集合A={x|1≤x≤4},B={x|x>2},那么A∪B=( )
| A. | (2,4) | B. | (2,4] | C. | [1,+∞) | D. | (2,+∞) |