题目内容
用min{a,b}表示a,b两个数中最小值,设f(x)=min{
,
}(x≥
),则由函数f(x)图象、x轴与直线x=
和直线x=2围成的封闭图形的面积是 .
| 1 |
| x |
| x |
| 1 |
| 4 |
| 1 |
| 4 |
考点:定积分在求面积中的应用
专题:导数的概念及应用
分析:先根据min{a,b}表示a,b两个数中的较小的数画出函数f(x)的图象,然后确定积分区间与被积函数,再求出定积分,即可求得封闭图形的面积.
解答:
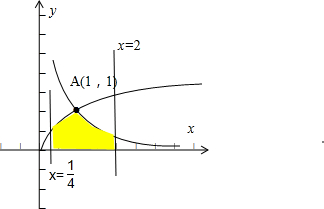 解:联立方程
解:联立方程
,可得交点坐标为A(1,1)
根据题意可得由函数y=f(x)的图象、x轴、直线x=
和直线x=2所围成的封闭图形的面积是
S=
dx+
dx=(
x
)
+(lnx)
=
-
+ln2=
+ln2.
故答案为:
+ln2.
 解:联立方程
解:联立方程
|
根据题意可得由函数y=f(x)的图象、x轴、直线x=
| 1 |
| 4 |
S=
| ∫ | 1
|
| x |
| ∫ | 2 1 |
| 1 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| | | 1
|
| | | 2 1 |
| 2 |
| 3 |
| 1 |
| 12 |
| 7 |
| 12 |
故答案为:
| 7 |
| 12 |
点评:本题重点考查封闭图形的面积,解题的关键是确定积分区间与被积函数,同时考查了分析问题的能力,属于中档题.

练习册系列答案
相关题目
已知二项式(2x-
)n展开式中的第5项为常数项,则展开式中各项的二项式系数之和为( )
| 1 | ||
|
| A、1 | B、32 | C、64 | D、128 |
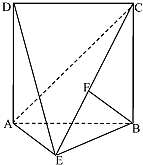 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在校CE上,无论点F运动到何处时,总有BF⊥AE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在校CE上,无论点F运动到何处时,总有BF⊥AE.