题目内容
已知（x2-x+1）n=a0+a1x+a2x2+…+a2nx2n（n∈N*），则a1+a2+a3+…+a2n-1= ．
考点：二项式系数的性质
专题：二项式定理
分析：由题意可得a0=1，a2n=1．在所给的等式中，令x=1，可得a0+a1+a2+a3+…+a2n-1+a2n=1，从而求得a1+a2+a3+…+a2n-1的值．
解答：
解：∵（x2-x+1）n=a0+a1x+a2x2+…+a2nx2n（n∈N*），
∴a0=1，a2n=1．
在（x2-x+1）n=a0+a1x+a2x2+…+a2nx2n（n∈N*）中，令x=1，
可得a0+a1+a2+a3+…+a2n-1+a2n=1，
∴a1+a2+a3+…+a2n-1=-1，
故答案为：-1．
∴a0=1，a2n=1．
在（x2-x+1）n=a0+a1x+a2x2+…+a2nx2n（n∈N*）中，令x=1，
可得a0+a1+a2+a3+…+a2n-1+a2n=1，
∴a1+a2+a3+…+a2n-1=-1，
故答案为：-1．
点评：本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于中档题．
练习册系列答案
相关题目
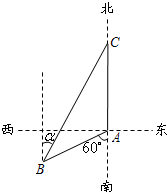如图所示，海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处，一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行．若海监船同时从B处出发，沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处．则海监船最少约用多长时间能追上渔船？过点（a，0）（a＞0）的直线与抛物线y2=4x交于A，B两点，在抛物线的准线x=-1上存在一点C，使得
•
最小时，a的值为（ ）
| CA |
| CB |
| A、1 | B、2 |
| C、4 | D、与直线的斜率有关 |