题目内容
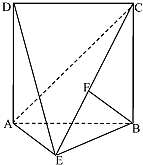 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在校CE上,无论点F运动到何处时,总有BF⊥AE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在校CE上,无论点F运动到何处时,总有BF⊥AE.(Ⅰ)试判断平面ADE与平面BCE是否垂直,并证明你的结论;
(Ⅱ)求二面角D-CE-A的余弦值的大小.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间角
分析:(Ⅰ)平面ADE⊥平面BCE.利用空间几何知识进行证明.
(Ⅱ)取AB中点O为原点,以OE为x轴,OB为y轴,过O垂直于平面ABE的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角D-CE-A的余弦值的大小.
(Ⅱ)取AB中点O为原点,以OE为x轴,OB为y轴,过O垂直于平面ABE的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角D-CE-A的余弦值的大小.
解答:
解:(Ⅰ)平面ADE⊥平面BCE.
∵动点F在棱CE上,无论点F运动到何处时,总有BF⊥AE,
∴AE⊥平面BCE,
∵AE?平面ADE,
∴平面ADE⊥平面BCE.
(Ⅱ)取AB中点O为原点,以OE为x轴,OB为y轴,过O垂直于平面ABE的直线为z轴,
建立空间直角坐标系,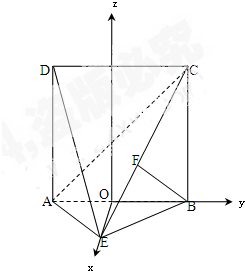
由题意知:A(0,-1,0),D(0,-1,2),
C(0,1,2),E(1,0,0),
=(0,2,0),
=(1,-1,-2),
=(1,1,0),
=(0,2,2),
设平面EDC的法向量
=(x,y,z),
则
,
取x=2,得
=(2,0,1),
设平面EAC的法向量
=(x1,y1,z1),
则
,
取x1=1,得
=(1,-1,1),
∴cos<
,
>=
=
.
∴二面角D-CE-A的余弦值的大小为
.
∵动点F在棱CE上,无论点F运动到何处时,总有BF⊥AE,
∴AE⊥平面BCE,
∵AE?平面ADE,
∴平面ADE⊥平面BCE.
(Ⅱ)取AB中点O为原点,以OE为x轴,OB为y轴,过O垂直于平面ABE的直线为z轴,
建立空间直角坐标系,

由题意知:A(0,-1,0),D(0,-1,2),
C(0,1,2),E(1,0,0),
| DC |
| CE |
| AE |
| AC |
设平面EDC的法向量
| n |
则
|
取x=2,得
| n |
设平面EAC的法向量
| m |
则
|
取x1=1,得
| m |
∴cos<
| n |
| m |
| 2+0+1 | ||||
|
| ||
| 5 |
∴二面角D-CE-A的余弦值的大小为
| ||
| 5 |
点评:本题考查平面与平面是否垂直的判断与证明,考查二面角的大小的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
已知集合A={x||x+1|<1},B={x|(
)x-2≥0},则A∩∁RB=( )
| 1 |
| 2 |
| A、(-2,-1) |
| B、(-2,-1] |
| C、(-1,0) |
| D、[-1,0) |
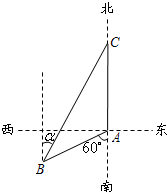 如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?
如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?