题目内容

如图，OA为圆C的直径，有向线段OB与圆C交于点P，且
OB
=
3
OP
，若|
OP
|=1，则
OA
•
OB
=
 
．
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：连接PA，则∠OPA=90°，运用向量的数量积的定义和解直角三角形的知识，即可得到所求值．
解答： 解：如图，连接PA，则∠OPA=90°，
由于
OB
=
3
OP
，若|
OP
|=1，
则
OA
•
OB
=
3
OP
•
OA
=
3
|
OP
|•|
OA
|•cos∠AOP
=
3
|
OA
|•cos∠AOP=
3
|
OP
|=
3
．
故答案为：
3
．
点评：本题考查平面向量的数量积的定义，考查圆的直径所对的角为直角，考查运算能力，属于基础题．
练习册系列答案
相关题目
如图所示程序的输出结果为s=132．则判断中应填
 
已知过点（0，1）的直线l：xtanα-y-3tanβ=0的一个法向量为（2，-1），则tan（α+β）=
 
．
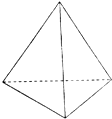
如图放置的六条棱长都相等的三棱锥，则这个几何体的侧视图是（　　）
A、等腰三角形
B、等边三角形
C、直角三角形
D、无两边相等的三角形
已知a=（
1
2
）-1，则二项式（1-
a
x
）5的展开式中x-2的系数为
 
．
已知一组数据为0，3，5，x，9，13，且这组数据的中位数为7，那么这组数据的众数为（　　）
A、13B、9C、7D、0
已知xlnx═-
1
e
，则x=
 
．
直线l经过两直线2x-y+4=0与x-y+5=0的交点，且与直线l1：x+y-6=0平行．
（1）求直线l的方程；
（2）若点 P（a，1）到直线l的距离与直线l1到直线l的距离相等，求实数a的值．
已知函数f（x）=
2-x，x≤0
log2x，0＜x≤2
2x-2，x＞2
，则f（
2
）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网