题目内容
2.已知点F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左焦点,点E是该双曲线的右焦点,过点F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是直角三角形,则该双曲线的离心率为1+$\sqrt{2}$.分析 利用双曲线的对称性及直角三角形,可得∠AEF=45°,从而|AF|=|EF|,求出|AF|,|EF|,得到关于a,b,c的等式,即可求出离心率的值和渐近线方程.
解答 解:∵△ABE是直角三角形,∴∠AEB为直角,
∵双曲线关于x轴对称,且直线AB垂直x轴,
∴∠AEF=∠BEF=45°,
∴|AF|=|EF|,
∵F为左焦点,设其坐标为(-c,0),
令x=-c,则$\frac{{c}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
则有y=±$\frac{{b}^{2}}{a}$,
∴|AF|=$\frac{{b}^{2}}{a}$,∴|EF|=2c,
∴$\frac{{b}^{2}}{a}$=2c
∴b2=2ac,
即c2-a2=2ac,
即∴e2-2e-1=0,
∵e>1,∴e=1+$\sqrt{2}$,
故答案为:1+$\sqrt{2}$.
点评 本题考查双曲线的对称性、考查双曲线的三参数关系:c2=a2+b2、考查双曲线的离心率和渐近线方程,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.双曲线$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 3 | D. | 6 |
10.已知双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的离心率$\sqrt{5}$,则该双曲线的一条渐近线被圆C:x2+y2-2x-3=0截得的弦长为( )
| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | $\frac{{8\sqrt{5}}}{5}$ | C. | 3 | D. | 2 |
17.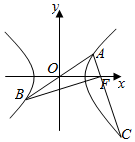 如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过坐标原点O,AC经过双曲线的右焦点F,若BF⊥AC,且|$\overrightarrow{AF}$|=a,则该双曲线的离心率是( )
如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过坐标原点O,AC经过双曲线的右焦点F,若BF⊥AC,且|$\overrightarrow{AF}$|=a,则该双曲线的离心率是( )
 如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过坐标原点O,AC经过双曲线的右焦点F,若BF⊥AC,且|$\overrightarrow{AF}$|=a,则该双曲线的离心率是( )
如图所示,A,B,C是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的三个点,AB经过坐标原点O,AC经过双曲线的右焦点F,若BF⊥AC,且|$\overrightarrow{AF}$|=a,则该双曲线的离心率是( )| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | $\frac{3}{2}$ | D. | 3 |
7.以正方形的一条边的两个端点为焦点,且过另外两个顶点的椭圆与双曲线的离心率之积为( )
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
14.抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,O为坐标原点.若|AF|=3,且△AOB的面积为$\frac{{3\sqrt{2}}}{2}$,则点B的纵坐标为( )
| A. | ±1 | B. | $±\frac{{\sqrt{2}}}{2}$ | C. | $±\sqrt{2}$ | D. | $±\frac{1}{2}$ |