题目内容

12．过点A（0，1）作直线，与双曲线${x^2}-\frac{y^2}{9}=1$有且只有一个公共点，则符合条件的直线的条数为（　　）
A．0B．2C．4D．无数

分析 用代数法，先联立方程，消元后得到一个方程，先研究相切的情况，即判别式等于零，再研究与渐近线平行的情况．

解答 解：设过点（0，1）与双曲线${x^2}-\frac{y^2}{9}=1$有且只有一个公共点的直线为y=kx+1．
根据题意：$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}-\frac{{y}^{2}}{9}=1}\end{array}\right.$，
消去y整理得（9-k2）x2-2kx-10=0，
∵△=0，
∴k=±$\sqrt{10}$．
又注意直线恒过点（0，1）且渐近线的斜率为±3，
与渐近线平行时也成立．
故过点（0，1）与双曲线${x^2}-\frac{y^2}{9}=1$有且只有一个公共点的直线有4条．
故选C．

点评 本题主要考查直线与双曲线的位置关系，在只有一个公共点时，不要忽视了与渐近线平行的情况．

练习册系列答案
相关题目
2．已知点F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左焦点，点E是该双曲线的右焦点，过点F且垂直于x轴的直线与双曲线交于A、B两点，△ABE是直角三角形，则该双曲线的离心率为1+$\sqrt{2}$．
3．已知函数$f（x）=\left\{\begin{array}{l}x+1（x≤1）\\ \sqrt{x}（x＞1）.\end{array}\right.$若f（x）＞f（x+1），则x的取值范围是（0，1]．
20．在平面直角坐标系xOy中，已知△ABC的顶点B、C恰好是双曲线M：$\frac{x^2}{9}-\frac{y^2}{16}=1$的左右焦点，且顶点A在双曲线M的右支上，则$\frac{sinC-sinB}{sinA}$=$\frac{3}{5}$．
7．设a，b是不相等的两个正数，且blna-alnb=a-b，给出下列结论：①a+b-ab＞1；②a+b＞2；③$\frac{1}{a}$+$\frac{1}{b}$＞2．其中所有正确结论的序号是（　　）
A．①②B．①③C．②③D．①②③
17．如图（1），在等腰梯形ABCD中，AB∥CD，E，F分别为AB和CD的中点，且AB=EF=2，CD=6，M为EC中点，现将梯形ABCD沿EF所在直线折起，使平面EFCB⊥平面EFDA，如图（2）所示，N是CD的中点．
（Ⅰ）求证：MN∥平面ADFE；
（Ⅱ）求四棱锥M-EFDA的体积．
4．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x，x＞0}\\{-{x}^{2}-2x，x≤0}\\{\;}\end{array}\right.$，则不等式f（x）≤0的解集为{x|x≥1或x=0或x≤-2}．
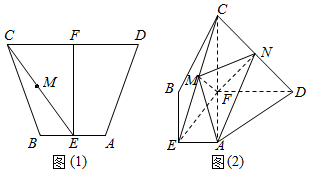
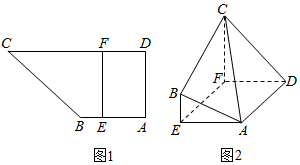1．如图1，直角梯形ABCD中，AB∥CD，∠BAD=90°，AB=AD=2，CD=4，点E为线段AB上异于A，B的点，且EF∥AD，沿EF将面EBCF折起，使平面EBCF⊥平面AEFD，如图2．
（Ⅰ）求证：AB∥平面DFC；
（Ⅱ）当三棱锥F-ABE体积最大时，求钝二面角B-AC-D的余弦值．
2．设复数z1，z2在复平面内的点关于实轴对称，z1=1+i，则$\frac{z_1}{z_2}$=（　　）
A．-iB．iC．-1D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网