题目内容
11.设不等式组$\left\{\begin{array}{l}x-y≤0\\ x+y≤4\\ x≥1\end{array}\right.$表示的平面区域为M,若直线l:y=k(x+2)上存在区域M内的点,则k的取值范围是$[\frac{1}{3},\;1]$.分析 作出不等式组对应的平面区域,根据直线和区域的关系即可得到结论.
解答  解:作出不等式组对应的平面区域,
解:作出不等式组对应的平面区域,
直线y=k(x+2)过定点D(-2,0),
由图象可知当直线l经过点A时,直线斜率最大,当经过点B时,直线斜率最小,
由$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,即A(1,3),此时k=$\frac{3}{1+2}$=$\frac{3}{3}=1$,
由$\left\{\begin{array}{l}{x=1}\\{x-y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,即B(1,1),此时k=$\frac{1}{1+2}$=$\frac{1}{3}$,
故k的取值范围是$[\frac{1}{3},\;1]$,
故答案为:$[\frac{1}{3},\;1]$
点评 本题主要考查线性规划的应用以及直线斜率的公式的计算,利用数形结合是解决此类问题的基本方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.一个六棱柱的底面是正六边形,侧棱垂直于底面,所有棱的长都为1,顶点都在同一个球面上,则该球的体积为( )
| A. | 20π | B. | $\frac{{20\sqrt{5}π}}{3}$ | C. | 5π | D. | $\frac{{5\sqrt{5}π}}{6}$ |
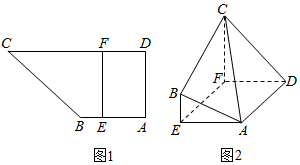 如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.
如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.