题目内容
已知集合A={x|x＜-1或x＞4}，B={x|2a≤x≤a+3}，若B⊆A，求实数a的取值范围．
考点：集合的包含关系判断及应用
专题：集合
分析：要分B等于空集和不等于空集两种情况．再根据B⊆A求出a的取值范围．
解答：
解：根据题意得：
当B=∅时，2a＞a+3，∴a＞3；
当B≠∅时，若2a=a+3，则a=3，B={6}，∴B⊆A，故a=3符合题意；
若a≠3，则，
或
；
∴解得，a＜-4，或2＜a＜3．
综上可得，实数a的取值范围为{a|a＜-4，或a＞2}．
当B=∅时，2a＞a+3，∴a＞3；
当B≠∅时，若2a=a+3，则a=3，B={6}，∴B⊆A，故a=3符合题意；
若a≠3，则，
|
|
∴解得，a＜-4，或2＜a＜3．
综上可得，实数a的取值范围为{a|a＜-4，或a＞2}．
点评：注意B=∅的情况，及2a=a+3的情况．要理解子集的定义．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
相关题目
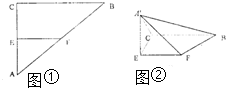
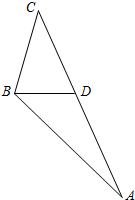近日我渔船编队在钓鱼岛附近点A周围海域作业，在B处的海监15船测得A在其南偏东45°方向上，测得渔政船310在其北偏东15°方向上，且与B的距离为4