Question

如图①，△ABC是等腰直角三角形，AC=BC=4，∠ACB=90°，E，F分别是AC，AB的中点，将△AEF折起，使点A到达A′位置，且A′在平面BCEF上的射影恰为点E，如图②．

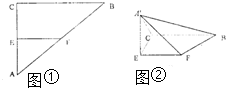
（1）求证EF⊥A′C；
（2）求点F到平面A′BC的距离．

Answer 1

考点：点、线、面间的距离计算,空间中直线与直线之间的位置关系

专题：空间位置关系与距离

分析：（1）由三角形中位线定理得EF∥BC，且EF⊥AC，从而EF⊥平面A′EC，由此能证明EF⊥A′C．
（2）由线面垂直得A′E⊥EC，由勾股定理得S△A′BC=

1

2

•A′C•BC=4

2

，设点F到平面A′BC的距离为d，由VF-A′BC=VA′-FBC，能求出点F到平面A′BC的距离．

解答： （1）证明：在等腰直角△ABC中，
∵E，F分别是AC、AB的中点，
∴EF∥BC，且BC⊥AC，∴EF⊥AC，
∴在四棱锥A′-BCEF中，
EF⊥A′E，EF⊥EC，
又∵A′E∩EC=E，A′E?平面A′EC，EC?平面A′EC，
∴EF⊥平面A′EC，∵A′C?平面A′EC，
∴EF⊥A′C．
（2）解：∵BC∥EF，∴由（1）得BC⊥A′C，
由已知得A′E⊥平面BCEF，
∴A′E⊥EC，
在Rt△A′CB中，A′C=

A′E2+EC2

=

4+4

=2

2

，BC=4，
∴S△A′BC=

1

2

•A′C•BC
=

1

2

×2

2

×4=4

2

，
设点F到平面A′BC的距离为d，
由VF-A′BC=VA′-FBC，得：

1

3

•S△ABC•d=

1

3

•S△FBC•A′E，
∴d=

S△FBC•A′E

S△A′BC

=

1 2 ×4×2×2

4 2

=

2

，
∴点F到平面A′BC的距离为

2

．

点评：本题考查异面直线垂直的证明，考查点到平面的距离的求法，解题时要认真审题，注意空间思维能力的培养．