题目内容
18.已知边长为2的菱形ABCD中,∠BCD=60°,E为DC的中点,如图1所示,将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,如图2所示.(Ⅰ)求证:△PAB为直角三角形;
(Ⅱ)求二面角A-PD-E的余弦值.

分析 (Ⅰ)推导出BE⊥DC,AB∥CD,从而AB⊥BE,进而∠ABE=90°,将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,在翻折过程中,∠ABE=90°不变,由此能证明△PAB为直角三角形.
(Ⅱ)以E为原点,ED为x轴,EB为y轴,EP为z轴,建立空间直角坐标系,利用向量法能求出二面角A-PD-E的余弦值.
解答 证明:(Ⅰ)∵边长为2的菱形ABCD中,∠BCD=60°,E为DC的中点,如图1所示,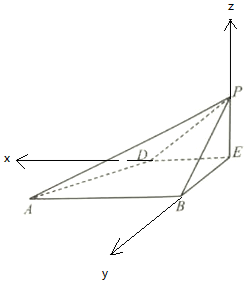
∴BE⊥DC,AB∥CD,∴AB⊥BE,∴∠ABE=90°,
∵将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,如图2所示.
在翻折过程中,∠ABE=90°不变,
∴在△ABP中,∠ABP=90°,
∴△PAB为直角三角形.
解:(Ⅱ)由(Ⅰ)得∠BED=∠ABE=90°,∴DE⊥BE,
以E为原点,ED为x轴,EB为y轴,EP为z轴,建立空间直角坐标系,
A(2,$\sqrt{3}$,0),P(0,0,1),D(1,0,0),E(0,0,0),
$\overrightarrow{DP}$=(-1,0,1),$\overrightarrow{DA}$=(1,$\sqrt{3}$,0),$\overrightarrow{EP}$=(0,0,1),$\overrightarrow{ED}$=(1,0,0),
设平面ADP的法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DA}=x+\sqrt{3}y=0}\\{\overrightarrow{m}•\overrightarrow{DP}=-x+z=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{m}$=($\sqrt{3},-1,\sqrt{3}$),
平面PDE的法向量$\overrightarrow{n}$=(1,0,0),
设二面角A-PD-E的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\sqrt{3}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$,
∴二面角A-PD-E的余弦值为$\frac{\sqrt{21}}{7}$.
点评 本题考查三角形为直角三角形的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想、函数与方程思想,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -2 | B. | -1 | C. | -4 | D. | -3 |
| A. | (-2,0]∪(2,+∞) | B. | (-2,+∞) | C. | (-∞,-2)∪(0,2) | D. | (-∞,2) |
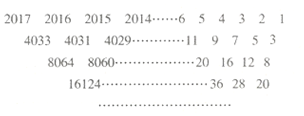 “杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )| A. | 2017×22016 | B. | 2018×22015 | C. | 2017×22015 | D. | 2018×22016 |
①?x∈R,2x>3x;②“x≠3”是“|x|≠3”成立的充分条件;③空间中若直线l若平行于平面α,则α内所有直线均与l是异面直线;④空间中有三个角是直角的四边形不一定是平面图形.
| A. | ①③ | B. | ①④ | C. | ②④ | D. | ②③ |
| A. | 0 | B. | 10 | C. | 12 | D. | 24 |
| A. | ab<ac | B. | ba>ca | C. | logab<logac | D. | $\frac{a}{b}>\frac{a}{c}$ |