题目内容
10．下列命题中，正确的是（ ）①?x∈R，2x＞3x；②“x≠3”是“|x|≠3”成立的充分条件；③空间中若直线l若平行于平面α，则α内所有直线均与l是异面直线；④空间中有三个角是直角的四边形不一定是平面图形．
| A． | ①③ | B． | ①④ | C． | ②④ | D． | ②③ |
分析 ①举例说明命题正确；
②由“x≠3”时，“|x|≠3”不成立，不是充分条件；
③由直线与平面平行的性质定理，判断命题错误；
④举例说明命题正确．
解答 解：对于①，当x=-1时，2-1=$\frac{1}{2}$＞$\frac{1}{3}$=3-1，∴①正确；
对于②，“x≠3”时，“|x|≠3”不成立，不是充分条件，②错误；
对于③，直线l平行于平面α，则过直线l的平面与平面α相交，
直线l与交线平行，∴③错误；
对于④，对角为直角的平面四边形沿着非直角所在的对角线翻折；
在翻折的过程中，某个瞬间出现了有三个直角的空间四边形，∴④正确．
综上，正确的命题是①④．
故选：B．
点评 本题考查了命题真假的判断问题，也考查了简易逻辑的应用问题，是基础题．
练习册系列答案
相关题目
20．已知在△ABC中，b2+a2-c2＜0，且b＞a，sinA+$\sqrt{2}$cosA=$\frac{5}{3}$，则tanA=（ ）
| A． | $\frac{2\sqrt{2}}{3}$或$\frac{4\sqrt{2}}{9}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{7\sqrt{2}}{8}$ | D． | $\frac{\sqrt{2}}{4}$或$\frac{7\sqrt{2}}{8}$ |
1．
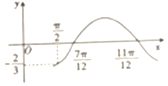已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的 部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，则f（$\frac{π}{3}$）等于（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的 部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，则f（$\frac{π}{3}$）等于（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{1}{2}$ | C． | -$\frac{\sqrt{2}}{4}$ | D． | $\frac{1}{4}$ |
15．已知命题$p：?x＞e，{（{\frac{1}{2}}）^x}$＞lnx；命题q：?a＞1，b＞1，logab+2logba≥2$\sqrt{2}$，则下列命题中为真命题的是（ ）
| A． | （?p）∧q | B． | p∧q | C． | p∧（?q） | D． | p∨（?q） |
2．在区间[0，2]上随机取两个数x，y，则xy∈[0，2]的概率是（ ）
| A． | $\frac{1-ln2}{2}$ | B． | $\frac{3-2ln2}{4}$ | C． | $\frac{1+ln2}{2}$ | D． | $\frac{1+2ln2}{2}$ |