题目内容
9．若函数f（x）=$\frac{1}{2}$x2+2x-3lnx+4a的极小值为-$\frac{3}{2}$，则a的值为（ ）| A． | -2 | B． | -1 | C． | -4 | D． | -3 |
分析 求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的极小值，求出a的值即可．
解答 解：函数的定义域为：x＞0；f′（x）=x+2-$\frac{3}{x}$，
令f′（x）＞0，解得：1＜x，
令f′（x）＜0，解得：0＜x＜1，
故f（x）在（0，1）递减，在（1，+∞）递增，
∴f（x）极小值=f（1）=$\frac{1}{2}+2+4a$=$-\frac{3}{2}$，解得：a=-1，
故选：B．
点评 本题考查了函数的单调性问题，考查导数的应用，是一道中档题．
练习册系列答案
相关题目
19．直线$\left\{\begin{array}{l}x=1+tcosα\\ y=-2+tsinα\end{array}$（t为参数，0≤a＜π）必过点（ ）
| A． | （1，-2） | B． | （-1，2） | C． | （-2，1） | D． | （2，-1） |
20．已知在△ABC中，b2+a2-c2＜0，且b＞a，sinA+$\sqrt{2}$cosA=$\frac{5}{3}$，则tanA=（ ）
| A． | $\frac{2\sqrt{2}}{3}$或$\frac{4\sqrt{2}}{9}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{7\sqrt{2}}{8}$ | D． | $\frac{\sqrt{2}}{4}$或$\frac{7\sqrt{2}}{8}$ |
4．A${\;}_{5}^{2}$-C${\;}_{5}^{3}$等于（ ）
| A． | 0 | B． | -10 | C． | 10 | D． | -40 |
1．
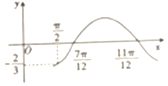已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的 部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，则f（$\frac{π}{3}$）等于（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的 部分图象如图所示，f（$\frac{π}{2}$）=-$\frac{2}{3}$，则f（$\frac{π}{3}$）等于（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{1}{2}$ | C． | -$\frac{\sqrt{2}}{4}$ | D． | $\frac{1}{4}$ |
