题目内容
公差不为零的等差数列{an}中,a3-a72+a11=0,数列{bn}是等比数列,且b7=a7,则b1•b2…b13等于 .
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:根据等差数列的性质化简已知条件,得到关于a7的方程,求出方程的解得到a7的值,进而得到b7的值,把所求的式子利用等比数列的性质化简,将b7的值代入即可求出值.
解答:
解:根据等差数列的性质得:a3+a11=2a7,
∵a3-a72+a11=0(已知),
∴2a7-a72=0,
解得a7=2,或a7=0(舍去),
∴b7=a7=2,又数列{bn}是等比数列,
则b1•b2…b13=b713=213=8192.
故答案为:8192.
∵a3-a72+a11=0(已知),
∴2a7-a72=0,
解得a7=2,或a7=0(舍去),
∴b7=a7=2,又数列{bn}是等比数列,
则b1•b2…b13=b713=213=8192.
故答案为:8192.
点评:本题考查学生灵活运用等差数列的性质及等比数列的性质化简求值,是一道基础题.

练习册系列答案
相关题目
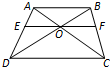 如图,在梯形ABCD中,AB∥CD,AB=3,CD=4.过AC与BD的交点O作EF∥AB,分别交AD,BC于点E,F,则EF=
如图,在梯形ABCD中,AB∥CD,AB=3,CD=4.过AC与BD的交点O作EF∥AB,分别交AD,BC于点E,F,则EF= 如图,已知△ABC的∠BAC的平分线与BC相交于点D,△ABC的外接圆的切线AE与BC的延长线相交于点E,若EB=8,EC=2,则ED=
如图,已知△ABC的∠BAC的平分线与BC相交于点D,△ABC的外接圆的切线AE与BC的延长线相交于点E,若EB=8,EC=2,则ED= 已知三次函数f(x)=ax3+bx2+cx+d(a≠0)的图象必有一个对称中心.判断其图象的对称中心的流程图如图所示.对于函数f(x)=
已知三次函数f(x)=ax3+bx2+cx+d(a≠0)的图象必有一个对称中心.判断其图象的对称中心的流程图如图所示.对于函数f(x)=