题目内容
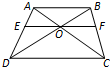如图，在梯形ABCD中，AB∥CD，AB=3，CD=4．过AC与BD的交点O作EF∥AB，分别交AD，BC于点E，F，则EF=考点：平行线分线段成比例定理
专题：选作题,立体几何
分析：由已知中EF∥AB∥DC，我们易得到△OAD∽△OCD，△OAE∽△CAD，进而我们可以求出AB，EF，DC三条平行线段分线段所成的比例，结合AB=3，CD=4，即可求出答案．
解答：
解：∵EF∥AB∥DC，
∴△OAB∽△OCD，△OAE∽△CAD
∴OA：OC=AB：DC=3：4
OE：DC=OA：CA=3：7
∴EF=2×
×4=
，
故答案为：
．
∴△OAB∽△OCD，△OAE∽△CAD
∴OA：OC=AB：DC=3：4
OE：DC=OA：CA=3：7
∴EF=2×
| 3 |
| 7 |
| 24 |
| 7 |
故答案为：
| 24 |
| 7 |
点评：本题考查的知识点是平等线分线段成比例定理，其中求出平行线分线段所成的比例是解答本题的关键．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
相关题目
已知数列{an}中a1=1，an+1=an+n，若利用如图所示的程序框图计算该数列的第8项，则判断框内的条件是