题目内容
已知曲线C:f(x)=x3-ax+a,若过曲线C外一点A(1,0)引曲线C的两条切线,它们的倾斜角互补,则a的值为( )
A、
| ||
| B、-2 | ||
| C、2 | ||
D、-
|
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,设出切点坐标,由点斜式得到切线方程,再由点A在且线上得到关于切点横坐标的方程,求得两切点,再由两切点处的导数互为相反数求得a的值.
解答:
解:由f(x)=x3-ax+a,得f′(x)=3x2-a,
设切点为(x0,x03-ax0+a),
∴f′(x0)=3x02-a,
∴过切点的切线方程为y-x03+ax0-a=(3x02-a)(x-x0),
∵切线过点A(1,0),
∴-x03+ax0-a=(3x02-a)(1-x0),
解得:x0=0或x0=
.
∴f′(0)=-a,f′(
)=
-a,
由两切线倾斜角互补,得
-a=a-
,
∴a=
.
故选:A.
设切点为(x0,x03-ax0+a),
∴f′(x0)=3x02-a,
∴过切点的切线方程为y-x03+ax0-a=(3x02-a)(x-x0),
∵切线过点A(1,0),
∴-x03+ax0-a=(3x02-a)(1-x0),
解得:x0=0或x0=
| 3 |
| 2 |
∴f′(0)=-a,f′(
| 3 |
| 2 |
| 27 |
| 4 |
由两切线倾斜角互补,得
-a=a-
| 27 |
| 4 |
∴a=
| 27 |
| 8 |
故选:A.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,关键是注意给出的点是否为切点,是中档题.

练习册系列答案
相关题目
P是圆(x-5)2+(y-3)2=9上点,则点P到直线3x+4y-2=0的最大距离是( )
| A、2 | B、5 | C、8 | D、9 |
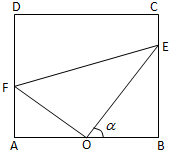 合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50
合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50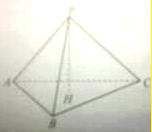 如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC于H,求证:H是△ABC的垂心,△ABC为锐角三角形.
如图,P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面ABC于H,求证:H是△ABC的垂心,△ABC为锐角三角形. 如图,△ABC中,AC=BC=
如图,△ABC中,AC=BC=