题目内容
已知函数f（x）=2ax-
在区间（0，1]上是增函数，则a的取值范围是 ．
| 1 |
| x2 |
考点：利用导数研究函数的单调性
专题：计算题,导数的综合应用
分析：求导f′（x）=2a+
，函数f（x）=2ax-
在区间（0，1]上是增函数可化为2a+
≥0在（0，1]上恒成立，从而化为最值问题．
| 2 |
| x3 |
| 1 |
| x2 |
| 2 |
| x3 |
解答：
解：∵f′（x）=2a+
，
若使函数f（x）=2ax-
在区间（0，1]上是增函数，
则2a+
≥0在（0，1]上恒成立，
又∵y=2a+
在（0，1]上是减函数，
∴2a+2≥0，
∴a≥-1．
故答案为：a≥-1．
| 2 |
| x3 |
若使函数f（x）=2ax-
| 1 |
| x2 |
则2a+
| 2 |
| x3 |
又∵y=2a+
| 2 |
| x3 |
∴2a+2≥0，
∴a≥-1．
故答案为：a≥-1．
点评：本题考查了导数的综合应用，同时考查了恒成立问题的处理方法，属于中档题．
练习册系列答案
相关题目
已知ABCD为矩形，平面PAB⊥平面ABCD，平面PAD⊥平面ABCD，M，N分别是AB，PC中点．求证：MN⊥AB．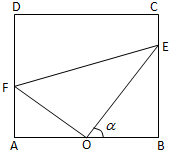
合肥一中生活区内建有一块矩形休闲区域ABCD，AB=100米，BC=50