题目内容
已知1∈{a，a+1，a2}，则实数a的可取值是（ ）
| A、0 | B、1 |
| C、-1 | D、0或1或-1 |
考点：元素与集合关系的判断
专题：计算题,集合
分析：由元素与集合的关系知，集合内的三个数有一个是1，注意集合中元素的互异性．
解答：
解：∵1∈{a，a+1，a2}，
∴若a=1，a2=1，故不成立；
若a+1=1，则a=0，a2=0，故不成立；
若a2=1，则a=-1或a=1；
若a=-1，则a+1=0，成立；
故选C．
∴若a=1，a2=1，故不成立；
若a+1=1，则a=0，a2=0，故不成立；
若a2=1，则a=-1或a=1；
若a=-1，则a+1=0，成立；
故选C．
点评：本题考查了元素与集合的关系应用及集合中元素的特征，属于基础题．
练习册系列答案
一本好题口算题卡系列答案
相关题目
设{an}是首项为-
，公差为d（d≠0）的等差数列，Sn为其前n项和，若S1，S2，S4成等比数列，则d=（ ）
| 1 |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
D、
|
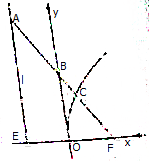如图，过抛物线y2=2px（p＞0）的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点，若| AB |
| BC |
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |