题目内容
已知函数f(x)=1+x-
+
-
+…+
,设F(x)=f(x+4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,圆x2+y2=b-a的面积的最小值是 .
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2015 |
| 2015 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,函数的性质及应用,导数的综合应用
分析:利用导数可判断f(x)在R上是增函数,利用零点判定定理可知f(x)的零点在[-1,0]内,从而F(x)的零点在[-5,-4]内,于是可得b-a的最小值为1,进而可得答案.
解答:
解:f′(x)=1-x+x2-x3+…+x2014=
>0(x≠-1,x≠0),
又f'(-1)=2015>0,f'(0)=1>0,
故f(x)在R上是增函数.
∵f(0)=1>0,f(-1)<0,
∴f(x)的零点在[-1,0]内,F(x)的零点在[-5,-4]内,b-a的最小值为1.
∴圆面积最小值为π.
故答案为:π.
| 1+x2015 |
| 1+x |
又f'(-1)=2015>0,f'(0)=1>0,
故f(x)在R上是增函数.
∵f(0)=1>0,f(-1)<0,
∴f(x)的零点在[-1,0]内,F(x)的零点在[-5,-4]内,b-a的最小值为1.
∴圆面积最小值为π.
故答案为:π.
点评:此题是难题.考查函数零点判定定理和利用导数研究函数的单调性以及数列求和问题以及函数图象的平移,体现了分类讨论的思想,以及学生灵活应用知识分析解决问题的能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设圆x2+y2=4的一条切线与x轴、y轴分别交于点A、B,则|AB|的最小值为( )
| A、4 | ||
B、4
| ||
| C、6 | ||
| D、8 |
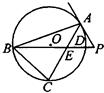 如图,△ABC是圆O的内接三角形,PA是圆O的切线,PB交AC于点E,交圆O于点D,若PA=PE,PB=9,PD=1,∠ABC=60°,则EC的长等于
如图,△ABC是圆O的内接三角形,PA是圆O的切线,PB交AC于点E,交圆O于点D,若PA=PE,PB=9,PD=1,∠ABC=60°,则EC的长等于