题目内容
已知(
-
)9的展开式中,x3的系数为
,则常数a的值为 .
| a |
| x |
|
| 9 |
| 4 |
考点:二项式系数的性质
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于0=3,求得r的值,即可求得展开式中x3的系数,再由x3的系数为
,求得a的值.
| 9 |
| 4 |
解答:
解:(
-
)9的展开式中,通项公式为 Tr+1=
•(
)-r•(-1)r•a9-r•x
-9,
令
-9=3,求得r=8,故x3的系数为
•
a=
,∴a=4,
故答案为:4.
| a |
| x |
|
| C | r 9 |
| 2 |
| 3r |
| 2 |
令
| 3r |
| 2 |
| C | 8 9 |
| 1 |
| 16 |
| 9 |
| 4 |
故答案为:4.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
正项等比数列{an}中,若2a48a52=16,则a1a99等于( )
| A、-16 | B、8 | C、16 | D、4 |
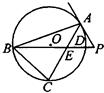 如图,△ABC是圆O的内接三角形,PA是圆O的切线,PB交AC于点E,交圆O于点D,若PA=PE,PB=9,PD=1,∠ABC=60°,则EC的长等于
如图,△ABC是圆O的内接三角形,PA是圆O的切线,PB交AC于点E,交圆O于点D,若PA=PE,PB=9,PD=1,∠ABC=60°,则EC的长等于