题目内容
已知实数x，y满足
，则z=x+y-2的取值范围是 ．
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合确定z的最大值．
解答：
解：令u=x+y，则y=-x+u，u表示直线y=-x+u
在y轴上的截距．作出不等式组表示的平面区域，
易知直线y=-x+u经过B（1，2）时，u有最大值3，
直线y=-x+u经过A（-2，1），u有最小值为-1，
因此z=x+y-2的取值范围是[-3，1]．
故答案为：[-3，1]
在y轴上的截距．作出不等式组表示的平面区域，
易知直线y=-x+u经过B（1，2）时，u有最大值3，
直线y=-x+u经过A（-2，1），u有最小值为-1，
因此z=x+y-2的取值范围是[-3，1]．
故答案为：[-3，1]
点评：本题主要考查线性规划的应用，结合目标函数的几何意义，利用数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
相关题目
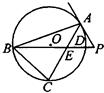如图，△ABC是圆O的内接三角形，PA是圆O的切线，PB交AC于点E，交圆O于点D，若PA=PE，PB=9，PD=1，∠ABC=60°，则EC的长等于