题目内容
已知Ω={（x，y）|3x+y≤4，x≥0，y≥0}，A={（x，y）|x≥y}，若向区域Ω内随机投入一点P，则点P落入区域A的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：计算题,概率与统计
分析：先明确是几何概型中的面积类型，分别求区域A={（x，y）|x≥y}和区域Ω={（x，y）|3x+y≤4，x≥0，y≥0}的面积，然后求比值即可．
解答：
解：如右图，直线3x+y=4和y=x的交点为C（1，1），
且A（
，0）、B（0，4），
故所求概率为P=
=
．
故选：C．
解：如右图，直线3x+y=4和y=x的交点为C（1，1），且A（
| 4 |
| 3 |
故所求概率为P=
| S△AOC |
| S△AOB |
| 1 |
| 4 |
故选：C．
点评：本题主要考查几何概型中的面积类型，基本方法是：分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积，两者求比值，即为概率．
练习册系列答案
黄冈创优卷系列答案
相关题目
已知x=log3e，y=log97，z=e
，则（ ）
| 1 |
| 2 |
| A、x＞y＞z |
| B、y＞z＞x |
| C、z＞y＞x |
| D、z＞x＞y |
集合A={y|y=lgx，x＞1}，B={-2，-1，1，2}，则∁RA∩B=（ ）
| A、[-2，-1] |
| B、（-∞，0] |
| C、{1，2} |
| D、{-2，-1} |
若集合A={y|0≤y＜2}，B={x|-1＜x＜1}，则A∩（∁RB）=（ ）
| A、{x|0≤x≤1} |
| B、{x|1≤x＜2} |
| C、{x|-1＜x≤0} |
| D、{x|0≤x＜1} |
下列函数中，既是奇函数又在其定义域内是增函数的是（ ）
| A、f（x）=cosx |
| B、f（x）=sinx+x |
| C、f（x）=x2+1 |
| D、f（x）=x3-3x |
已知集合 A={0，1，2，3}，集合 B={x∈N||x|≤2}，则A∩B=?（ ）
| A、{ 3 } |
| B、{0，1，2} |
| C、{ 1，2} |
| D、{0，1，2，3} |
已知点P（a，b）与点Q（1，0）在直线2x+3y-1=0的两侧，且a＞0，b＞0，则
的取值范围是（ ）
| a-1 |
| b |
| A、（-∞，-3） | ||
B、(-
| ||
| C、（3，+∞） | ||
D、(0，
|
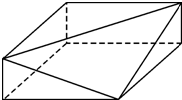某几何体的直观图如图所示，该几何体的主（正）视图和左（侧）视图都正确的是（ ）
