题目内容
已知命题p：函数f（x）=（m-2）x为增函数；命题q：方程x2+2mx+2-m=0有实根；若p假q真，求m的取值范围．
考点：复合命题的真假
专题：转化思想
分析：本题先根据命题p，利用函数的单调性，求出参数m的取值范围，再根据方程有实根，求出参数m的取值范围，最后求交集，得到本题的结论．
解答：
解：∵命题p：函数f（x）=（m-2）x为增函数，
∴若命题p为真命题，则有：m-2＞1，
∴m＞3．
∵命题q：方程x2+2mx+2-m=0有实根，
∴若命题q为真命题，则有：
△=4m2-4（2-m）≥0，
∴m≤-2或m≥1．
∵p假q真，
∴
，
∴m≤-2或1≤m≤3．
∴若命题p为真命题，则有：m-2＞1，
∴m＞3．
∵命题q：方程x2+2mx+2-m=0有实根，
∴若命题q为真命题，则有：
△=4m2-4（2-m）≥0，
∴m≤-2或m≥1．
∵p假q真，
∴
|
∴m≤-2或1≤m≤3．
点评：本题考查的是真假命题的性质，还考查了方程有实数的和函数的单调性，有一定的综合性，但整体难度不大，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
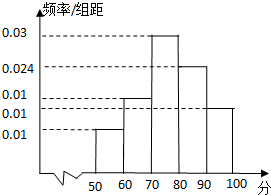某校为了解高一期末数学考试的情况，从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析，得到数学成绩频率分布直方图（如图所示），其中成绩在[50，60）的学生人数为6．