题目内容
已知点P（a，b）与点Q（1，0）在直线2x+3y-1=0的两侧，且a＞0，b＞0，则
的取值范围是（ ）
| a-1 |
| b |
| A、（-∞，-3） | ||
B、(-
| ||
| C、（3，+∞） | ||
D、(0，
|
考点：简单线性规划的应用,简单线性规划
专题：不等式的解法及应用
分析：由点P（a，b）与点Q（1，0）在直线2x+3y-1=0的两侧，可得（2a+3b-1）（2-1）＜0，即2a+3b-1＜0．又a＞0，b＞0，画出可行域．
=
表示可行域内的点（b，a）与点M（0，1）的斜率k．即可得出．
| a-1 |
| b |
| a-1 |
| b-0 |
解答：
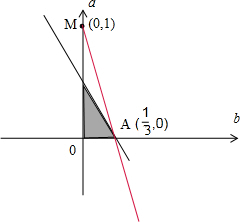解：∵点P（a，b）与点Q（1，0）在直线2x+3y-1=0的两侧
∴（2a+3b-1）（2-1）＜0，即2a+3b-1＜0．
又a＞0，b＞0，画出可行域：
=
表示可行域内的点（b，a）与点M（0，1）的斜率k．
当点M与（
，0）时，kAM=
=-3．
∴k＜kAM=-3．
因此
的取值范围是（-∞，-3）．
故选：A．
解：∵点P（a，b）与点Q（1，0）在直线2x+3y-1=0的两侧∴（2a+3b-1）（2-1）＜0，即2a+3b-1＜0．
又a＞0，b＞0，画出可行域：
| a-1 |
| b |
| a-1 |
| b-0 |
当点M与（
| 1 |
| 3 |
| 1-0 | ||
0-
|
∴k＜kAM=-3．
因此
| a-1 |
| b |
故选：A．
点评：本题考查了线性规划问题、直线的斜率计算公式及其单调性，考查了问题的转化能力和推理能力，属于中档题．
练习册系列答案
相关题目
若a＜1，那么（ ）
A、
| ||
| B、|a|＜1 | ||
| C、a2＜1 | ||
| D、a3＜1 |
已知集合A={1，2}，B={a，a2，2}，若A∩B={1，2}，则a的值为（ ）
| A、1 | ||
| B、-1 | ||
| C、±1 | ||
D、-
|
一个几何体的三视图如图所示，主视图与侧视图都是边长为2的正三角形，俯视图为正方形，则该几何体的全面积为（ ）
| A、4 | ||
| B、8 | ||
| C、12 | ||
D、4+4
|
已知函数f（x）=-
x3+2ax2+3x（a＞0）的导数f′（x）的最大值为5，则在函数f（x）图象上的点（1，f（1））处的切线方程是（ ）
| 2 |
| 3 |
| A、3x-15y+4=0 |
| B、15x-3y-2=0 |
| C、15x-3y+2=0 |
| D、3x-y+1=0 |
实数x，y满足条件
，则22x-y的最小值为（ ）
|
A、
| ||
B、
| ||
| C、1 | ||
| D、4 |
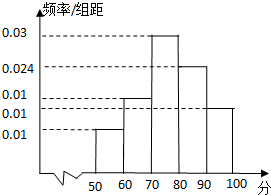某校为了解高一期末数学考试的情况，从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析，得到数学成绩频率分布直方图（如图所示），其中成绩在[50，60）的学生人数为6．