题目内容

已知直线y=k（x-1）与抛物线y2=4x交于点A（x1，y1），B（x2，y2），且x1+x2=4，则|AB|等于（　　）
A、4B、6C、8D、10
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：求出直线系经过的定点，利用抛物线的性质求解就．
解答： 解：由条件易知直线过抛物线的焦点F（1，0），则|AB|=|AF|+|BF|=x1+x2+2=6．
故选：B．
点评：本题考查直线与抛物线的位置关系，抛物线的基本性质的应用，考查计算能力．
练习册系列答案
相关题目
已知两圆C1：x2+y2=4，C2：x2+y2-2x-4y+4=0，直线l：x+2y=0，
（1）求经过圆C1、C2的交点且和直线l相切的圆的方程；
（2）若实数x，y满足（1）中所求圆的方程，求
y
x
的最大值，2y-x的最小值．
函数f（x）=1+logax（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny-2=0上，则m2+n2的最小值为
 
．
已知矩形ABCD的顶点都在半径为R的球O的球面上，AB=6，BC=2
3
，棱锥O-ABCD的体积为8
3
，则球O的表面积为（　　）
A、16πB、32
C、48πD、64π
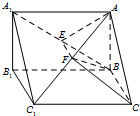如图，在直三棱柱A1B1C1-ABC中，AB⊥BC，E、F分别是A1B，AC1的中点．
（1）求证：EF∥平面ABC；
（2）求证：平面AEF⊥平面AA1B1B；
（3）若AB=BC=a，A1A=2a，求三棱锥F-ABC的体积．
根据下列条件，求圆锥曲线的标准方程．
（1）顶点在原点，对称轴为y轴，顶点到准线的距离为4的抛物线；
（2）中心在坐标原点，焦点在坐标轴上且过点P（-2，0），Q（3，
5
2
）的双曲线．
如图，正六边形ABCDEF的边长为
3
，则
AC
•
DB
=
 
函数y=
1
2
x-1，x∈[-2，4]的值域y∈
 
．
已知数列{an}的前n项和Sn=2（an-1），求数列{an}的通项公式为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网