题目内容
已知α为锐角，且tanα=
-1，函数f（x）=x2tan2α+x•sin（2α+
），则f（-1）= ．
| 2 |
| π |
| 4 |
考点：三角函数的化简求值
专题：计算题
分析：由tan2α=
，将tanα=
-1代入可求解，由α为锐角，得α，进而求得函数表达式．确定f（-1）的值
| 2tanα |
| 1-tan2α |
| 2 |
解答：
解：∵tan2α=
=
=1
又∵α为锐角
∴α=
∴sin（2α+
）=1
∴f（x）=x2+x
f（-1）=（-1）2-1=0．
故答案为：0．
| 2tanα |
| 1-tan2α |
2
| ||
1-(
|
又∵α为锐角
∴α=
| π |
| 8 |
| π |
| 4 |
∴f（x）=x2+x
f（-1）=（-1）2-1=0．
故答案为：0．
点评：本题主要考查倍角公式，求函数解析式，考查计算能力．
练习册系列答案
相关题目
ξ～N（1，0.04）P（ξ＞1）=（ ）
| A、0.2 | B、0.3 |
| C、0.4 | D、0.5 |
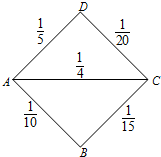某先生居住在城镇的A处，准备开车到单位C处上班，若该地各路段发生堵车事件都是相互独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如下图（例如，路段AB发生堵车事件的概率为