题目内容
已知函数f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若x,y∈[-1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.
(1)判断f(x)的单调性,并加以证明;
(2)解不等式f(x+
)<f(1-2x);
(3)若f(x)≤m2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立.求实数m的取值范围.
(1)判断f(x)的单调性,并加以证明;
(2)解不等式f(x+
| 1 |
| 2 |
(3)若f(x)≤m2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立.求实数m的取值范围.
考点:函数恒成立问题,奇偶性与单调性的综合
专题:计算题,综合题
分析:(1)设x1,x2∈[-1,1],且x1<x2,则x1-x2<0,利用x,y∈[-1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0,可得f(x1)+f(-x2)<0,根据函数f(x)是定义在[-1,1]上的奇函数,即可得函数f(x)在[-1,1]上单调增;
(2)由(1)知,-1≤x+
<1-2x≤1,解之即可;
(3)先确定函数f(x)在[-1,1]上的最大值为f(1)=1,将f(x)≤m2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立转化为:0≤m2-2am对所有a∈[-1,1]恒成立,从而可求实数m的取值范围.
(2)由(1)知,-1≤x+
| 1 |
| 2 |
(3)先确定函数f(x)在[-1,1]上的最大值为f(1)=1,将f(x)≤m2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立转化为:0≤m2-2am对所有a∈[-1,1]恒成立,从而可求实数m的取值范围.
解答:
解:(1)函数f(x)在[-1,1]上单调增,证明如下
由题意,设x1,x2∈[-1,1],且x1<x2
则x1-x2<0
∵x,y∈[-1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.
令x=x1,y=-x2,
∴f(x1)+f(-x2)<0
∵函数f(x)是定义在[-1,1]上的奇函数
∴f(x1)-f(x2)<0
∴函数f(x)在[-1,1]上单调增;
(2)由(1)知,-1≤x+
<1-2x≤1,解得:0≤x<
(3)由于函数f(x)在[-1,1]上单调增,
∴函数f(x)在[-1,1]上的最大值为f(1)=1
∴f(x)≤m2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立可转化为:0≤m2-2am对所有a∈[-1,1]恒成立
∴
,
解得m≥2或m≤-2或m=0
由题意,设x1,x2∈[-1,1],且x1<x2
则x1-x2<0
∵x,y∈[-1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.
令x=x1,y=-x2,
∴f(x1)+f(-x2)<0
∵函数f(x)是定义在[-1,1]上的奇函数
∴f(x1)-f(x2)<0
∴函数f(x)在[-1,1]上单调增;
(2)由(1)知,-1≤x+
| 1 |
| 2 |
| 1 |
| 6 |
(3)由于函数f(x)在[-1,1]上单调增,
∴函数f(x)在[-1,1]上的最大值为f(1)=1
∴f(x)≤m2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立可转化为:0≤m2-2am对所有a∈[-1,1]恒成立
∴
|
解得m≥2或m≤-2或m=0
点评:本题以抽象函数的性质为载体,考查函数的单调性,考查单调性与奇偶性的结合,同时考查了恒成立问题,解题的关键是:f(x)≤m2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立转化为:0≤m2-2am对所有a∈[-1,1]恒成立

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
ξ~N(1,0.04)P(ξ>1)=( )
| A、0.2 | B、0.3 |
| C、0.4 | D、0.5 |
方程组
共有( )组解.
|
| A、1 | B、2 | C、3 | D、4 |
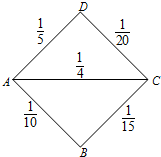 某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为