题目内容
设空间被分为5个不交的非空集合,证明:一定有一个平面,它至少与其中的四个集合有公共点.
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:如图所示,四个平行平面,α,β,γ,Ω.把空间分为5个不交的非空集合,可得与平面α相交的平面π,也一定与其它三个平面相交.
解答:
证明:如图所示,四个平行平面,α,β,γ,Ω.
把空间分为5个不交的非空集合,
则与平面α相交的平面π,也一定与其它三个平面相交.
因此:一定有一个平面,它至少与其中的四个集合有公共点.

把空间分为5个不交的非空集合,
则与平面α相交的平面π,也一定与其它三个平面相交.
因此:一定有一个平面,它至少与其中的四个集合有公共点.
点评:本题考查了平面的划分、平行平面与相交平面,考查了推理能力,属于基础题.

练习册系列答案
相关题目
在△ABC中,若A=60°,a=
,b=2
则满足条件的△ABC( )
| 5 |
| 2 |
| A、不存在 | B、有一个 |
| C、有两个 | D、个数不确定 |
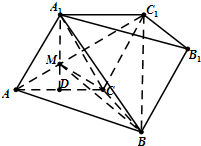 已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.
已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.