Question

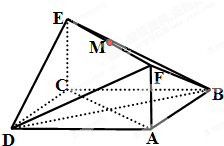如图所示，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=

2

，AF=1，M是线段EF的中点．
（1）证明：CM∥平面BDF；
（2）求四面体DEFB的体积．

Answer 1

考点：直线与平面平行的判定,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离,空间角

分析：（1）通过证明CM∥OF，进一步证明CM∥平面BDF
（2）平面ACEF⊥平面ABCD正方形对角线AC⊥BD，∴OD⊥平面ACEF同理可得：OB是四棱锥B-ACEF的高，进一步可证：AF是三棱锥F-ABD的高，EC是三棱锥E-CBD的高在正方形ABCD中，AC=BD=2，进一步利用分割法
求出四面体的体积．

解答： 证明：连结AC，BD交于点O，连结OF
∴O是AC的中点，
∵M是EF的中点，
∴CO∥MF，CO=MF
∴四边形OCMF是平行四边形．
∴CM∥OF
∵CM?平面BDF，OF?平面BDF
∴CM∥平面BDF
（2）∵平面ACEF⊥平面ABCD
正方形对角线AC⊥BD
∴OD⊥平面ACEF
同理可得：OB是四棱锥B-ACEF的高
进一步可证：AF是三棱锥F-ABD的高，EC是三棱锥E-CBD的高
在正方形ABCD中，AC=BD=2
∴OD=OB=1
V_{四面体DEFB}=V_{四棱锥D-ACEF}+V_{四棱锥B-ACEF}-V_{三棱锥F-ABD}-V_{三棱锥E-CBD}
=

1

3

OD•AF•AC+

1

3

OB•AF•AC-

1

3

AF•(

1

2

AD•AB)-

1

3

EC•(

1

2

CD•CB）
=

2

3

点评：本题考查的知识要点：线面平行的判定，面面垂直的性质定理，以及分割法在体积运算公式中的运算．