题目内容
已知函数f(x)=
,若|f(x)|≥ax,则a的取值范围是( )
|
| A、(-∞,0] |
| B、(-∞,1] |
| C、[-2,1] |
| D、[-2,0] |
考点:对数函数的单调性与特殊点
专题:函数的性质及应用
分析:依题意,作出y=|f(x)|与y=ax的图象,由图分析当x<0时,g(x)=|f(x)|=-(-x2+2x)=x2-2x,g′(x)|x=0=(2x-2)|x=0=-2,当-2≤a≤0时,|f(x)|≥ax,
于是可得答案.
于是可得答案.
解答:
解:∵f(x)=
,
∴y=|f(x)|与y=ax的图象如下:
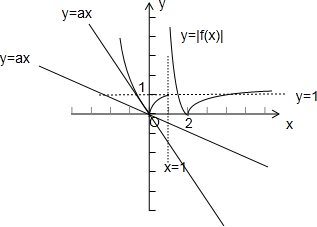
由图可知,当x<0时,g(x)=|f(x)|=-(-x2+2x)=x2-2x,
g′(x)|x=0=(2x-2)|x=0=-2,
∴当-2≤a≤0时,|f(x)|≥ax,
故选:D.
|
∴y=|f(x)|与y=ax的图象如下:

由图可知,当x<0时,g(x)=|f(x)|=-(-x2+2x)=x2-2x,
g′(x)|x=0=(2x-2)|x=0=-2,
∴当-2≤a≤0时,|f(x)|≥ax,
故选:D.
点评:本题考查对数函数的单调性与特殊点,考查分段函数的作图与函数恒成立问题,考查导数的几何意义,属于难题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
若直线l不平行于平面α,且l?α,则( )
| A、α内的所有直线与l异面 |
| B、α内不存在与l平行的直线 |
| C、α内存在唯一的直线与l平行 |
| D、α内的直线与l都相交 |
在△ABC中,若A=60°,a=
,b=2
则满足条件的△ABC( )
| 5 |
| 2 |
| A、不存在 | B、有一个 |
| C、有两个 | D、个数不确定 |
已知函数f(x)=2sin(ωx+ϕ) (其中ω>0,|ϕ|<
)的图象的相邻两条对称轴间的距离是
,且f(0)=
,则ω和ϕ的值分别是( )
| π |
| 2 |
| π |
| 2 |
| 3 |
A、2,
| ||
B、2,
| ||
C、4,
| ||
D、4,
|
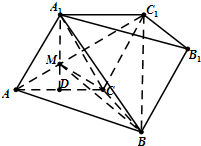 已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.
已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.