题目内容
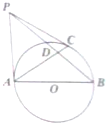如图，已知AB为圆O的直径，PA、PC是圆O的切线，A、C为切点，∠BAC=30°，PB交圆O于点D．（1）求∠APC的大小；
（2）若PA=
| 21 |
考点：与圆有关的比例线段
专题：直线与圆
分析：（1）由切线性质得∠BAP=90°，PA=PC，由此能求出∠APC=60°．
（2）由已知条件得到AC=PA=
，∠ACB=90°，由此利用切割线定理能求出PD．
（2）由已知条件得到AC=PA=
| 21 |
解答：
解：（1）∵PA是⊙O的切线，AB为⊙O的直径，
∴∠BAP=90°．∵∠BAC=30°，
∴∠CAP=∠PAB-∠CAB=60°．…（2分）
∵PA、PC是⊙O的切线，∴PA=PC，
∴△PAC是等边三角形．…（4分）
∴∠APC=60°（5分）
（2）∵△PAC是等边三角形，
∴AC=PA=
，…（6分）
∵AB是⊙O的直径，∴∠ACB=90°…（7分）
连接BC，在直角△ABC中，∵∠BAC=30°，∴AB=2
，…（8分）
∴在直角△PAB中，PB=
=7，…（9分）
∵PA是⊙O的切线，∴PA2=PD•PB，…（11分）
∴21=PD×7，解得PD=3．…（12分）
∴∠BAP=90°．∵∠BAC=30°，
∴∠CAP=∠PAB-∠CAB=60°．…（2分）
∵PA、PC是⊙O的切线，∴PA=PC，
∴△PAC是等边三角形．…（4分）
∴∠APC=60°（5分）
（2）∵△PAC是等边三角形，
∴AC=PA=
| 21 |
∵AB是⊙O的直径，∴∠ACB=90°…（7分）
连接BC，在直角△ABC中，∵∠BAC=30°，∴AB=2
| 7 |
∴在直角△PAB中，PB=
| PA2+AB2 |
∵PA是⊙O的切线，∴PA2=PD•PB，…（11分）
∴21=PD×7，解得PD=3．…（12分）
点评：本题考查角的大小的求法，考查线段长的求法，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
如图，矩形ABCD所在的平面和平面ABEF互相垂直，等腰梯形ABEF中，AB∥EF，AB=2，AD=AF=1，∠BAF=60°，O，P分别为AB，CB的中点，M为底面△OBF的重心．
如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直．AB∥CD，AB⊥BC，AB=2CD=2BC=2，EA⊥EB．
某同学将一块底边长为5的等腰直角三角板按如图所示的方式放置在平面直角坐标系上，其中∠OMN=