题目内容

若母线长是4的圆锥的轴截面的面积是8，求圆锥的高．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：利用已知条件求出圆锥的顶角，然后求解圆锥的高．
解答： 解：母线长是4的圆锥的轴截面的面积是8，
所以S=
1
2
AB•AC•sin∠BAC，8=
1
2
×4×4×sin∠BAC
∴sin∠BAC=1，则∠DAC=45°，
∴AD=ABcos45°=2
2
．
圆锥的高为：2
2
．
点评：本题考查旋转体的应用，轴截面以及三角形面积，空间几何体的高的求法，基本知识的应用．
练习册系列答案
相关题目
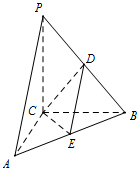如图，在三棱锥P-ABC中，PB⊥AC，PC⊥平面ABC，点D，E分别为线段PB，AB的中点．
（1）求证：AC⊥平面PBC；
（2）设二面角D-CE-B的平面角为θ，若PC=BC=2，AC=2
3
，求cosθ的值．
设数列{an}的各项均为正数，它的前n项的和为Sn，点（an，Sn）在函数y=
1
8
x2+
1
2
x+
1
2
的图象上；数列{bn}满足b1=a1，bn+1（an+1-an）=bn．其中n∈N*．
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）设cn=
an
bn
，求证：数列{cn}的前n项的和Tn＞
5
9
（n∈N*）．
已知数列{an}的前n项和为Sn，且Sn=n2+2n．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）数列{bn}中，b1=1，bn=2bn-1+1（n≥2），求{bn}的通项公式；
（Ⅲ）若cn=an（bn+1），求数列{cn}前几项和Tn．
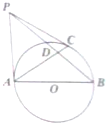如图，已知AB为圆O的直径，PA、PC是圆O的切线，A、C为切点，∠BAC=30°，PB交圆O于点D．
（1）求∠APC的大小；
（2）若PA=
21
，求PD的长．
已知双曲线C：
x2
a2
-
y2
b2
=1离心率是
2
，过点（
3
，1），且右支上的弦AB过右焦点F．
（1）求双曲线C的方程；
（2）求弦AB的中点M的轨迹E的方程；
（3）是否存在以AB为直径的圆过原点O？，若存在，求出直线AB的斜率k的值．若不存在，则说明理由．
某企业主要生产甲、乙两种品牌的空调，由于受到空调在保修期内维修费等因素的影响，企业生产每台空调的利润与该空调首次出现故障的时间有关，甲、乙两种品牌空调的保修期均为3年，现从该厂已售出的两种品牌空调中各随机抽取50台，统计数据如下：
品牌甲乙
首次出现故障时间
x年		0＜x≤11＜x≤22＜x≤3x＞30＜x≤22＜x≤3x＞3
空调数量（台）124432345
每台利润（千元）122.52.71.52.62.8
将频率视为概率，解答下列问题：
（Ⅰ）从该厂生产的甲品牌空调中随机抽取一台，求首次出现故障发生在保修期内的概率；
（Ⅱ）若该厂生产的空调均能售出，记生产一台甲品牌空调的利润为X1，生产一台乙品牌空调的利润为X2，分别求X1，X2的分布列；
（Ⅲ）该厂预计今后这两种品牌空调销量相当，但由于资金限制，只能生产其中一种品牌空调，若从经济效益的角度考虑，你认为应该生产哪种品牌的空调？说明理由．
已知函数f（x），g（x）都定义在实数集R上，且满足f（x）为奇函数，g（x）为偶函数，f（x）+g（x）=x2+x-2，试求函数f（x），g（x）的解析式．
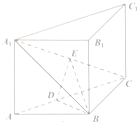如图，在三棱柱ABC-A1B1C1中，侧棱A1A⊥底面ABC，AB⊥BC，E是A1C的中点，D在线段AC上，并且DE⊥A1C，已知A1A=AB=
2
，BC=2．
（1）求证：A1C⊥平面EDB．
（2）求三棱锥E-BCD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网