题目内容
直线y=2x+2上的动点(an,an+1),n∈N*与定点(2,-3)所成直线的斜率为bn,且a1=3,
(1)求数列{an}的通项公式;
(2)证明:2<bn+1<bn≤11;
(3)证明:
+
+
+…
<2n.
(1)求数列{an}的通项公式;
(2)证明:2<bn+1<bn≤11;
(3)证明:
| 1 |
| b1-2 |
| 1 |
| b2-2 |
| 1 |
| b3-2 |
| 1 |
| bn-2 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知条件得an+1=2an+2,从而推导出
=2,又a1+2=3+2=5,由此求出an=5•2n-1-2.
(2)由已知条件得bn=
=
=2×
=2+
>2.由此能证明2<bn+1<bn≤11.
(3)由
=
=
•2n-
,能证明
+
+
+…
<2n.
| an+1+2 |
| an+2 |
(2)由已知条件得bn=
| an+1+3 |
| an-2 |
| 5•2n+1 |
| 5•2n-1-4 |
| 5•2n-8+9 |
| 5•2n-8 |
| 18 |
| 5•2n-8 |
(3)由
| 1 |
| bn-2 |
| 5•2n-8 |
| 18 |
| 5 |
| 18 |
| 4 |
| 9 |
| 1 |
| b1-2 |
| 1 |
| b2-2 |
| 1 |
| b3-2 |
| 1 |
| bn-2 |
解答:
(1)解:∵直线y=2x+2上的动点(an,an+1),n∈N*,
∴an+1=2an+2,n∈N*,∴an+1+2=2(an+2),
∴
=2,又a1+2=3+2=5,
∴{an+2}是首项为5,公比为2的等比数列,
∴an+2=5•2n-1,
∴an=5•2n-1-2.
(2)证明:∵动点(an,an+1),n∈N*与定点(2,-3)所成直线的斜率为bn,
∴bn=
=
=2×
=2+
>2.
∴{bn}是减数列,且bn>2,(bn)max=b1=2+
=11,
∴2<bn+1<bn≤11.
(3)证明:∵
=
=
•2n-
,
∴
+
+
+…
=
(2+22+…+2n)-
n
=
×
-
n
=
×2n-
-
n<2n.
∴
+
+
+…
<2n.
∴an+1=2an+2,n∈N*,∴an+1+2=2(an+2),
∴
| an+1+2 |
| an+2 |
∴{an+2}是首项为5,公比为2的等比数列,
∴an+2=5•2n-1,
∴an=5•2n-1-2.
(2)证明:∵动点(an,an+1),n∈N*与定点(2,-3)所成直线的斜率为bn,
∴bn=
| an+1+3 |
| an-2 |
| 5•2n+1 |
| 5•2n-1-4 |
| 5•2n-8+9 |
| 5•2n-8 |
| 18 |
| 5•2n-8 |
∴{bn}是减数列,且bn>2,(bn)max=b1=2+
| 18 |
| 5×2-8 |
∴2<bn+1<bn≤11.
(3)证明:∵
| 1 |
| bn-2 |
| 5•2n-8 |
| 18 |
| 5 |
| 18 |
| 4 |
| 9 |
∴
| 1 |
| b1-2 |
| 1 |
| b2-2 |
| 1 |
| b3-2 |
| 1 |
| bn-2 |
=
| 5 |
| 18 |
| 4 |
| 9 |
=
| 5 |
| 18 |
| 2(1-2n) |
| 1-2 |
| 4 |
| 9 |
=
| 5 |
| 9 |
| 5 |
| 9 |
| 4 |
| 9 |
∴
| 1 |
| b1-2 |
| 1 |
| b2-2 |
| 1 |
| b3-2 |
| 1 |
| bn-2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意分离变量法的合理运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
直线l1:(
-1)x+y-2=0与直线l2:(
+1)x-y-3=0的位置关系是( )
| 2 |
| 2 |
| A、平行 | B、相交 | C、垂直 | D、重合 |
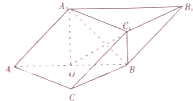 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.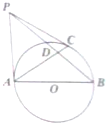 如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D.
如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D. 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=1,∠ACB=90°,AA1=2,M,N分别是棱CC1,AB中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=1,∠ACB=90°,AA1=2,M,N分别是棱CC1,AB中点.