题目内容
已知二次函数f(x)=ax2+bx+c(a>0).
(Ⅰ)(i)若b=-2,且f(x)在(1,+∞)上为单调递增函数,求实数a的取值范围;
(ii)若b=-1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,求实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,求a的最小正整数值.
(Ⅰ)(i)若b=-2,且f(x)在(1,+∞)上为单调递增函数,求实数a的取值范围;
(ii)若b=-1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,求实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,求a的最小正整数值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)(i)若b=-2,f(x)在(1,+∞)上为单调递增函数,则
≤1,解得实数a的取值范围;
(ii)若b=-1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,则
或
,解得实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,则
,解得实数a的取值范围;
| 1 |
| a |
(ii)若b=-1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,则
|
|
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,则
|
解答:
解:(Ⅰ)(i)若b=-2,
则f(x)=ax2-2x+c(a>0)的图象是开口朝上且以直线x=
为对称轴的抛物线.
若f(x)在(1,+∞)上为单调递增函数,
则
≤1,
解得a≥1,
即实数a的取值范围为[1,+∞)
(ii)若b=-1,c=1,
则f(x)=ax2-x+1(a>0)的图象是开口朝上且以直线x=
为对称轴的抛物线.
若当x∈[0,1]时,|f(x)|的最大值为1,
则
或
,
解得0<a<
,或
≤a≤1
综上所述:0<a≤1
即实数a的取值范围为(0,1]
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,
则
由b2>4ac>4a(1-a-b)得:
b2+4ab+4a2=(b+2a)2>4a,
即b+2a>2
,
即b>2
-2a,…①
由b2>4ac≥4a得:
b<-2
…②
由①②得:
2
-2a<-2
,
解得a>4,
故a的最小正整数值为5.
则f(x)=ax2-2x+c(a>0)的图象是开口朝上且以直线x=
| 1 |
| a |
若f(x)在(1,+∞)上为单调递增函数,
则
| 1 |
| a |
解得a≥1,
即实数a的取值范围为[1,+∞)
(ii)若b=-1,c=1,
则f(x)=ax2-x+1(a>0)的图象是开口朝上且以直线x=
| 1 |
| 2a |
若当x∈[0,1]时,|f(x)|的最大值为1,
则
|
|
解得0<a<
| 1 |
| 2 |
| 1 |
| 2 |
综上所述:0<a≤1
即实数a的取值范围为(0,1]
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,
则
|
由b2>4ac>4a(1-a-b)得:
b2+4ab+4a2=(b+2a)2>4a,
即b+2a>2
| a |
即b>2
| a |
由b2>4ac≥4a得:
b<-2
| a |
由①②得:
2
| a |
| a |
解得a>4,
故a的最小正整数值为5.
点评:本题考查的知识点是二次函数的图象和性质,函数的单调性,函数的最值,难度中档.

练习册系列答案
相关题目
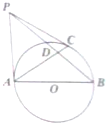 如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D.
如图,已知AB为圆O的直径,PA、PC是圆O的切线,A、C为切点,∠BAC=30°,PB交圆O于点D. 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中, 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=1,∠ACB=90°,AA1=2,M,N分别是棱CC1,AB中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=1,∠ACB=90°,AA1=2,M,N分别是棱CC1,AB中点.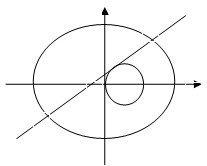 已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,
已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,